216. 组合总和 III
回溯终止条件是已选择的路径长度为 k,且和等于 n,此时找到一个解,并将其添加进结果集中。
每层回溯要做的事就是遍历可选的结果集,选择一个值去深入,然后回溯。
class Solution {
List<List<Integer>> res;
LinkedList<Integer> path;
public List<List<Integer>> combinationSum3(int k, int n) {
res = new LinkedList<>();
path = new LinkedList<>();
backtrace(n, k, 1);
return res;
}
public void backtrace(int n, int k, int start) {
// 这里采用的是减法,当 n 减为 0,说明 path 是满足条件的
if (path.size() == k && n == 0) {
res.add(new LinkedList<>(path));
return;
}
for (int i = start; i <= 9; i++) {
// 选中 i
// n 减去 i
n -= i;
// 加入到已选择的路径
path.add(i);
// 递归
backtrace(n, k, i + 1);
// n 加回 i
n += i;
// 从已选择路径中弹出
path.removeLast();
}
}
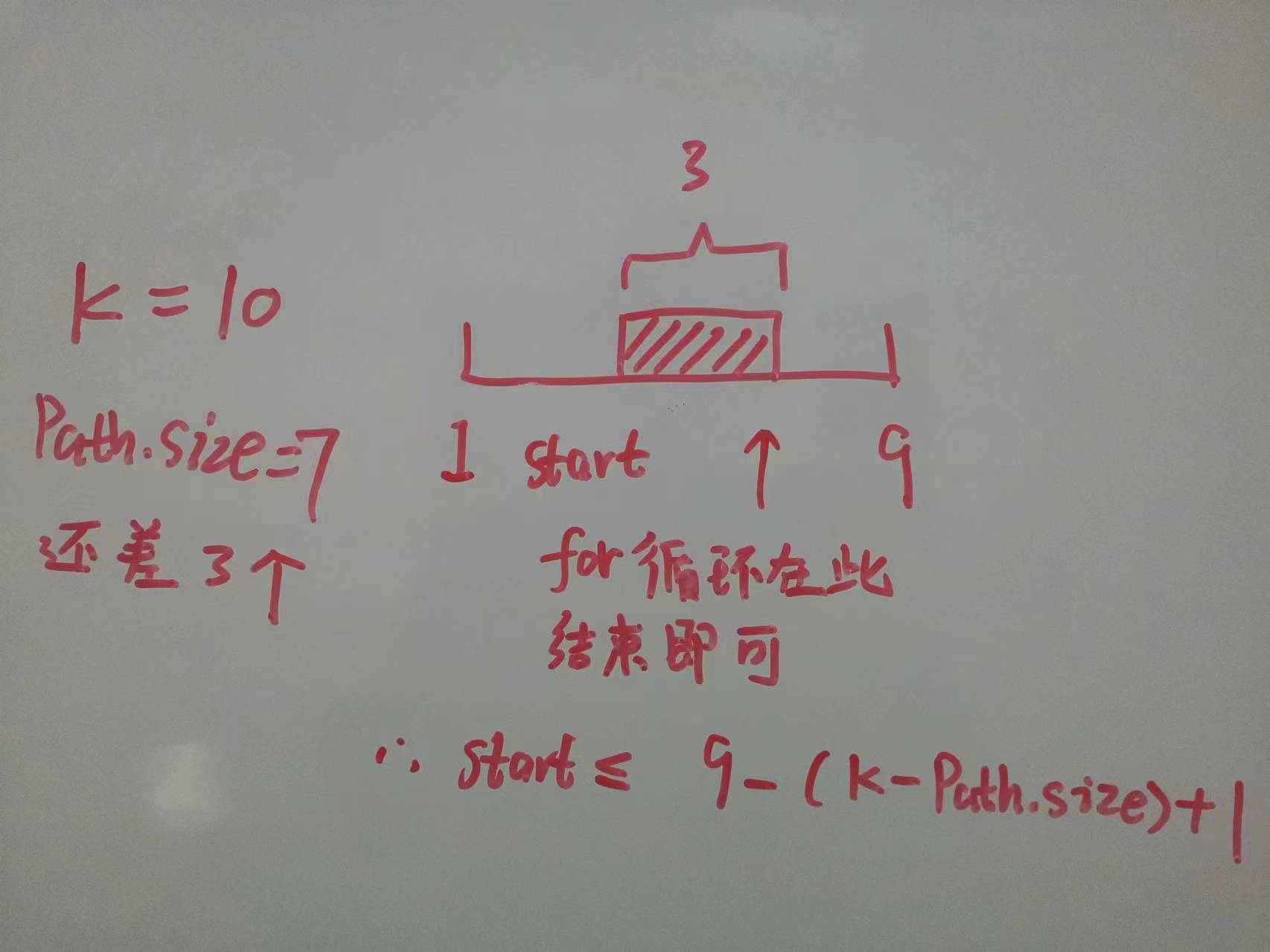
}上述代码也有一些优化点,主要从两方面考虑。一个是求和,题目规定了和的大小为 n,如果 path 中已选择元素的和大于 n,,如上来就是 5、6、7、8、9,大于要求的和 4,所以直接返回即可,不用深入递归。另一个是元素的个数,题目要求的个数是 k,也就是 path 的长度要求是 k,这就要求 for 循环中的结束条件是有限制的,不能无脑的到 9,得根据当前 path 的长度做计算,即 path 中已有 path.size() 个元素,那么还需要 k - path.size() 个元素,因此 start 的最大值应该是 9 - (k - path.size()) + 1。
public void backtrace(int n, int k, int start) {
// 优化 1,从和的角度考虑,如果当前的数比较大 n - i 直接干成负数了,那也不用递归了
if (n < 0) return;
if (path.size() == k && n == 0) {
res.add(new LinkedList<>(path));
return;
}
// 优化 2,从要求的元素个数考虑,取 9 不够 2 个
for (int i = start; i <= 9 + 1 - k + path.size(); i++) {
// for (int i = start; i <= 9; i++) {
n -= i;
path.add(i);
backtrace(n, k, i + 1);
n += i;
path.removeLast();
}
}17. 电话号码的字母组合
先用 map 将数字和字母的映射存起来。假如 digits 为 "234",选择顺序则应该是先从 2 对应的字母中选择,再从 3 对应的字母中选择,然后再从 4 对应的字母中选择。这就告诉我们 for 循环遍历的是数字对应的字母集合,具体是哪个数字,就按照上面提到的顺序读取从 digits 中读取。结束条件是 path 的长度和 digits 的长度相等。

class Solution {
private List<String> res;
private LinkedList<Character> path;
private Map<Character, char[]> map;
public List<String> letterCombinations(String digits) {
res = new LinkedList<>();
if (digits.isEmpty()) return res;
path = new LinkedList<>();
map = new HashMap<>();
map.put('2', new char[]{'a', 'b', 'c'});
map.put('3', new char[]{'d', 'e', 'f'});
map.put('4', new char[]{'g', 'h', 'i'});
map.put('5', new char[]{'j', 'k', 'l'});
map.put('6', new char[]{'m', 'n', 'o'});
map.put('7', new char[]{'p', 'q', 'r', 's'});
map.put('8', new char[]{'t', 'u', 'v'});
map.put('9', new char[]{'w', 'x', 'y', 'z'});
backtrace(digits, 0);
return res;
}
public void backtrace(String digits, int startIndex) {
if (path.size() == digits.length()) {
StringBuilder sb = new StringBuilder();
for (char c: path) sb.append(c);
res.add(sb.toString());
return;
}
// 根据 startIndex 决定读取哪个数字
char digit = digits.charAt(startIndex);
// 读取该数字对应的字母集合
char[] arr = map.get(digit);
// 从字母集合中选择字母
for (char elem: arr) {
path.add(elem);
// 递归,该读取 digits 中的下一个数字了
backtrace(digits, startIndex + 1);
path.removeLast();
}
}
}穷举,没什么优化空间。