代码随想录算法训练营第二十四天 | 回溯算法理论基础、组合

理论基础

回溯算法就是暴力穷举，本质是封装了一层类似于 for 循环的代码，通过递归调用，避免了 for 嵌套地狱的出现，实际上执行效率并不高。回溯函数就是递归函数。

回溯算法一般用来解决在集合中的查找问题，回溯算法解决的问题可以抽象为树形结构（N 叉树），集合的大小决定了树的宽度，递归的深度构成了树的深度，如图：

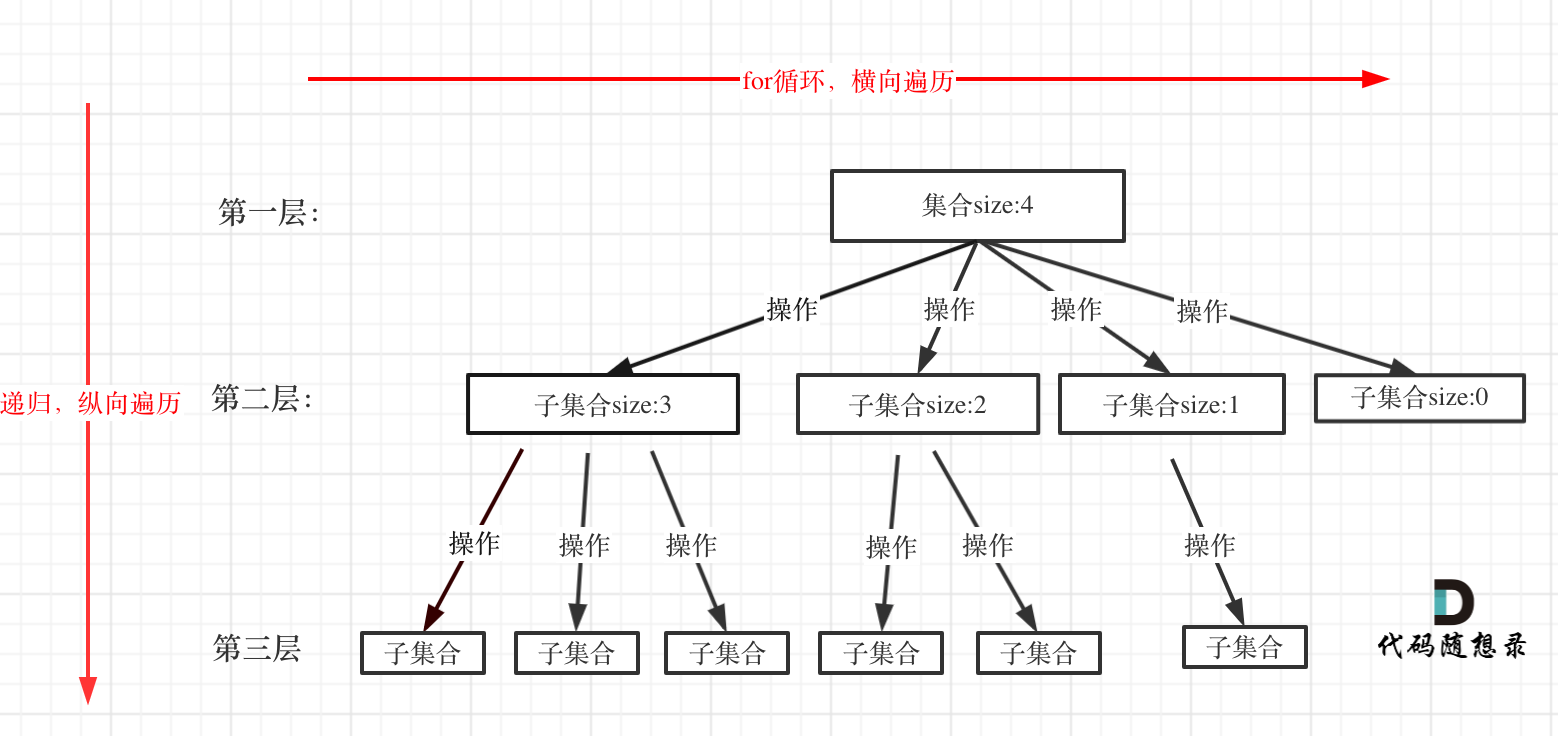
图片来源于代码随想录，图中的节点表示的是集合，可供选择的集合，可能会随着选择而不断缩减，路径表示在做的选择。

站在一个节点上，要考虑三个事情：

1. 路径：即已做出的选择
2. 选择列表：当前可以做的选择
3. 结束条件：到达决策树的底层，无法再做选择的条件

每个节点都可以理解为人生的岔路口，并附带有两个属性，一个是已经做的决策（路径），一个是可以做的决策（选择列表），现在要做的就是做出决策。

回溯算法模板

void backtrace(选择集合，已做出的选择) {
    if (终止条件) {
        // 收集结果
        // return
    }

    for (遍历集合) {
        将元素从集合中移除
        处理元素（加入选择）

        // 递归，开始下一层的选择，类似于执行嵌套的循环
        backtrace(选择集合，已做的决策)

        撤销处理（移出选择）
        将元素再加入集合
    }
}

77. 组合

leetcode
文档题解
视频题解

一般使用一个列表来存储每次选择的值，也方便回溯。但要注意 List 是引用类型的值，因此每次保存结果时要重新构造一个列表。

因为是组合，所以 [1, 2]、[2, 1] 是同一个结果，所以在选择 2 时就不能再选择 1，因此深入时需要不断的缩减集合，使用 start 标志选择的起始位置。

public class Solution {
    private LinkedList<Integer> path;
    private List<List<Integer>> res;

    public List<List<Integer>> combine(int n, int k) {
        path = new LinkedList<>();
        res = new LinkedList<>();
        backtrace(n, k, 1);
        return res;
    }

    // 每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围，就是要靠 start
    public void backtrace(int n, int k, int start) {
        if (path.size() == k) {
            // 根据已有 list，创建新的 list，如果直接 add(path) 的话，最终都是修改的同一个 path
            res.add(new LinkedList<>(path));
            return;
        }

        // 横向遍历, 从集合中选择元素
        for (int i = start; i <= n; i++) {
            // 深入
            path.add(i);
            // 纵向递归
            backtrace(n, k, i + 1);
            // 回溯
            path.removeLast();
        }
    }
}

46. 全排列

class Solution {
    List<List<Integer>> res;
    LinkedList<Integer> path;
    // 记录哪些元素已被使用
    boolean[] used;

    public List<List<Integer>> permute(int[] nums) {
        res = new LinkedList<>();
        path = new LinkedList<>();
        used = new boolean[nums.length];
        backtrace(nums);
        return res;
    }

    public void backtrace(int[] nums) {
        if (path.size() == nums.length) {
            res.add(new LinkedList<>(path));
            return;
        }

        for (int i = 0; i < nums.length; i++) {
            // 过滤掉已经在 path 中的元素
            if (used[i]) continue;
            used[i] = true;
            path.add(nums[i]);
            backtrace(nums);
            path.removeLast();
            used[i] = false;
        }
    }
}

参考资料

回溯算法解题套路框架