代码随想录算法训练营第三十八天 | 斐波那契数、爬楼梯、使用最小花费爬楼梯

509. 斐波那契数

leetcode
文档题解
视频题解

class Solution {
    public int fib(int n) {
        // 当 n 是 0、1 时的解
        if (n <= 1) return n;
        // 定义 dp 数组，保存递推的结果
        // dp[i] 表示第 i 个斐波那契数
        // 因为数列有第 0 个数，所以 dp 数组长度为 n + 1
        int[] dp = new int[n + 1];
        // 题目给出了递推公式: F(n) = F(n - 1) + F(n - 2)
        // 初始化 dp 数组
        dp[0] = 0;
        dp[1] = 1;
        // 根据递推公式可知当前的斐波那契数是前两个数相加得到的
        // 因此可以确定 dp 数组的遍历顺序，从前往后
        for (int i = 2; i <= n; i++) {
            // 根据递推公式求解
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

时间复杂度: O(n)
空间复杂度: O(n)

class Solution {
    public int fib(int n) {
        if (n <= 1) return n;
        int a = 0;
        int b = 1;
        for (int i = 2; i <= n; i++) {
            int tmp = a + b;
            a = b;
            b = tmp;
        }
        return b;
    }
}

时间复杂度: O(n)
空间复杂度: O(1)

class Solution {
    public int fib(int n) {
        if (n < 2) return n;
        return fib(n - 1) + fib(n - 2);
    }
}

时间复杂度: O(2^n)，画下递归图就知道了，是个 n 层的二叉树
空间复杂度: O(n)，递归栈空间

70. 爬楼梯

leetcode
文档题解
视频题解

决策问题，暴力回溯，超时，淦。

class Solution {
    int count = 0;
    public int climbStairs(int n) {
        backtrace(n);
        return count;
    }
    public void backtrace(int n) {
        if (n < 0) return;
        if (n == 0) {
            count++;
            return;
        }
        backtrace(n - 1);
        backtrace(n - 2);
    }
}

根据决策图，我们可以看到一丝端倪。

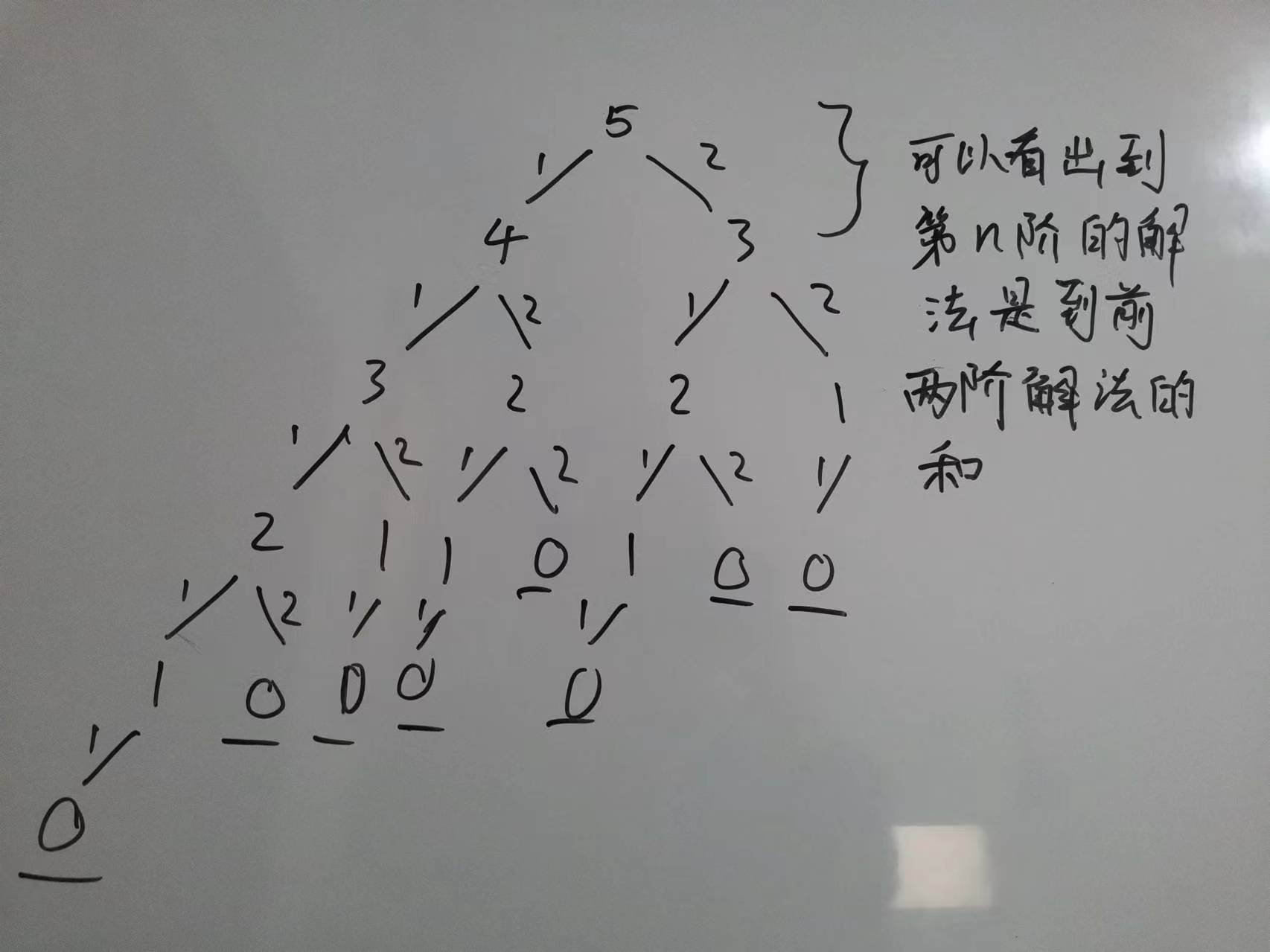
class Solution {
    public int climbStairs(int n) {
        if (n <= 2) return n;
        // 定义 dp 数组
        // dp[i] 表示到达第 i 阶有 dp[i] 种解法
        int[] dp = new int[n + 1];
        // 根据决策图，得递推公式 F(n) = F(n - 1) + F(n - 2)
        // 初始化，到达第一阶有一种解法，到达第二阶有两种解法
        dp[1] = 1;
        dp[2] = 2;
        // 根据递推公式，知道到达第 i 阶的解法和前两阶有关，所以从前往后遍历，构建 dp 数组
        for (int i = 3; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

746. 使用最小花费爬楼梯

leetcode
文档题解
视频题解

决策题，暴力回溯，超时，淦！

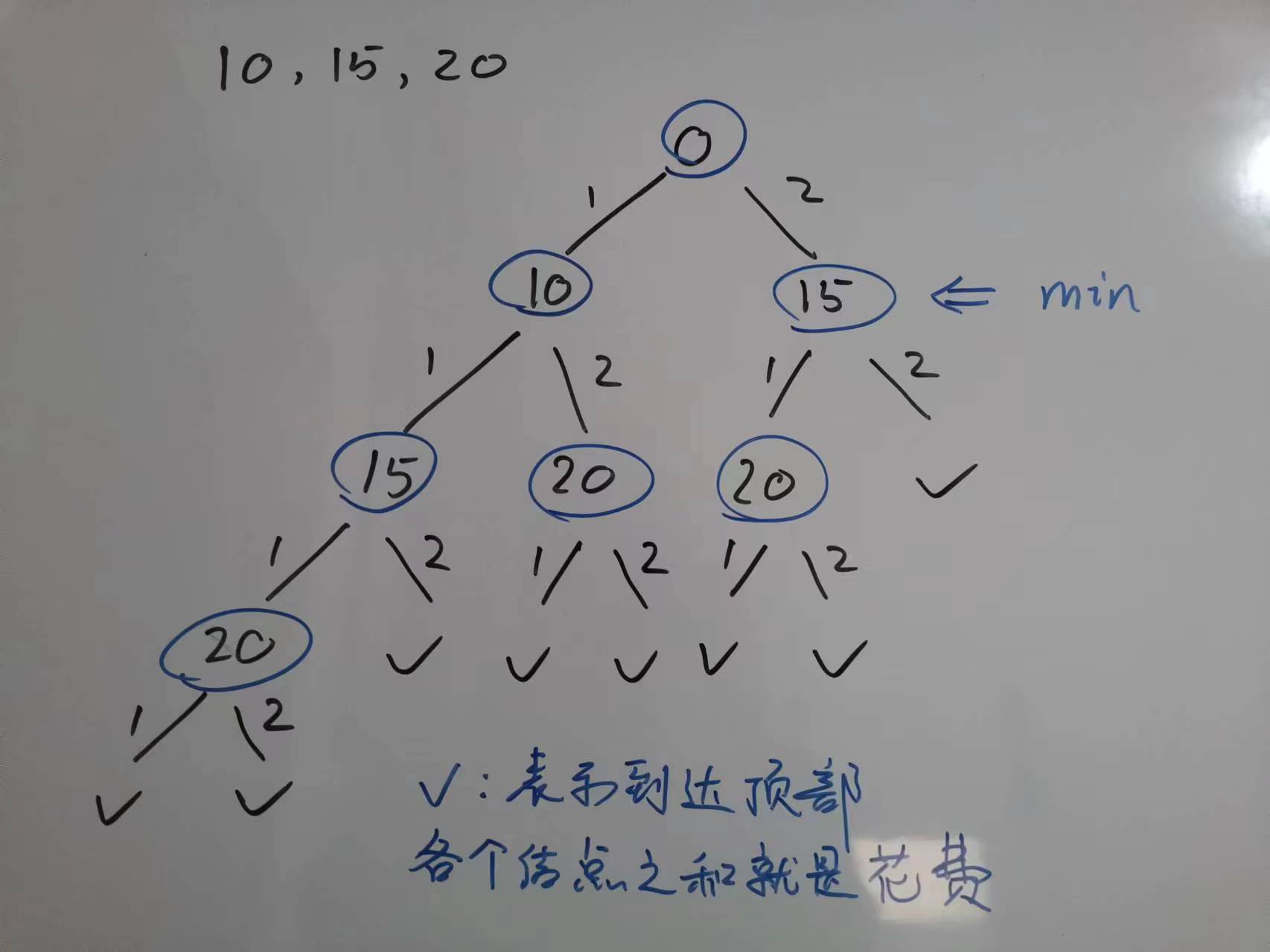
class Solution {
    int min = Integer.MAX_VALUE;
    public int minCostClimbingStairs(int[] cost) {
        backtrace(cost, -1, 0);
        return min;
    }
    // sum 是从上一步跳到 i 的花费
    public void backtrace(int[] cost, int i, int sum) {
        if (i >= cost.length) {
            min = Math.min(min, sum);
            return;
        };

        // 从 i 起跳的花费
        int _cost = i == -1 ? 0 : cost[i];
        for (int j = 1; j <= 2; j++) {
            backtrace(cost, i + j, sum + _cost);
        }
    }
}

动态规划，确定 dp[i] 的定义：dp[i] 表示到达第 i 阶所需的最小花费！

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        if (cost.length < 2) return 0;
        // 定义 dp 数组
        // dp[i] 表示到达第 i 阶所需的最小花费
        int[] dp = new int[cost.length + 1];
        // 因为第 i 层可以从 i - 1 一次跳一下跳过来
        // 也可以从 i - 2 一次跳两下跳过来
        // 因此递推公式为 F(n) = Min(F(n - 1), F(n - 2))
        // 初始化 dp 数组
        dp[0] = 0;
        dp[1] = 0;
        // 从前往后遍历
        for (int i = 2; i < dp.length; i++) {
            // 跳到 i 的花费等于跳到前一步的花费加上前一步往后跳的花费
            // 即 dp[前] + cost[前]，然后选择花费较小的
            dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i  -2]);
        }
        return dp[cost.length];
    }
}