977.有序数组的平方
这个题目非常容易踩的坑就是只考虑大于等于零的数,没考虑负数的平方可能会大于原数组中某些值的情况。好在 leetcode 中有负数的示例,能让大家缓过头来。
OK,接下来画个图方便大家理解。

原数组是非递减的顺序,平方之后负数部分是非递增的,正数部分是非递减的,如图所示,是一个凹下去的曲线,那么数组平方后的较大值就在两端,最小值就在中间。因此我们可以使用双指针的解法,从两端开始相向遍历,找到较大值放进结果数组。
为什么是找 left,right 中的较大值?因为我们确定数组平方后的两边是存在最大值的,可能是原来的最大值,也可能是负数平方后的最大值,因此每次循环都能确定当前区间的最大值。如果是找 left,right 中的较小值的话是不能保证其是该区间的最小值的。
class Solution {
public int[] sortedSquares(int[] nums) {
// 定义结果数组
int[] res = new int[nums.length];
// 定义指针,开始相向遍历
int left = 0, right = nums.length - 1, idx = res.length - 1;
// left right 相等时,表明要处理最后一个元素
while (left <= right) {
int left2 = nums[left] * nums[left];
int right2 = nums[right] * nums[right];
// 找到平方值的较大者,放进结果数组
if (left2 > right2) {
res[idx--] = left2;
left++;
} else {
res[idx--] = right2;
right--;
}
}
return res;
}
}209.长度最小的子数组
对于这种连续序列(数组、字符串)的问题,一般采用 “滑动窗口” 的处理方式,窗口内容就是连续序列。
滑动窗口的重点:何时扩大窗口,何时缩小窗口。
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int minLen = Integer.MAX_VALUE;
int left = 0, right = 0;
int sum = 0;
while (right < nums.length && left <= right) {
// 扩大窗口
sum += nums[right];
// 满足解的条件,因此当前窗口内的内容是一个解
while (sum >= target) {
// 更新解
minLen = Math.min(minLen, right - left + 1);
// 缩小窗口,看剩余内容还能否组成解
sum -= nums[left];
left++;
}
right++;
}
return minLen == Integer.MAX_VALUE ? 0 : minLen;
}
}59. 螺旋矩阵
这是一个纯数组下标操作的问题,模拟走路转向,按照螺旋的顺序不断填充值即可。也可以理解为涂色的游戏,已被涂色的值不能再去操作。
class Solution {
public int[][] generateMatrix(int n) {
// 结果数组
int[][] res = new int[n][n];
// 填充的值,从 1 开始
int cnt = 1;
// 定义每次填充的边界,每填充完一边,更改一次界限
int top = 0, bottom = n - 1;
int left = 0, right = n - 1;
// 按照螺旋顺序填充
// 填充到 n * n 结束
while (cnt <= n * n) {
// 先填充上面一层,从 left 到 right,top 不变
for (int i = left; i <= right; i++) {
res[top][i] = cnt++;
}
// 上面一层填充完毕,更改上界
top++;
// 再填充右边一层,从 top 到 bottom,right 不变
for (int i = top; i <= bottom; i++) {
res[i][right] = cnt++;
}
// 右边一层填充完毕,更改右界
right--;
// 再填充下面一层,从 right 到 left,bottom 不变
for (int i = right; i >= left; i--) {
res[bottom][i] = cnt++;
}
// 下面一层填充完毕,更改下界
bottom--;
// 再填充左边一层,从 bottom 到 top,left 不变
for (int i = bottom; i >= top; i--) {
res[i][left] = cnt++;
}
// 左边一层填充完毕,更改左界
left++;
}
return res;
}
}while 循环的本质是每次处理一层,如图:
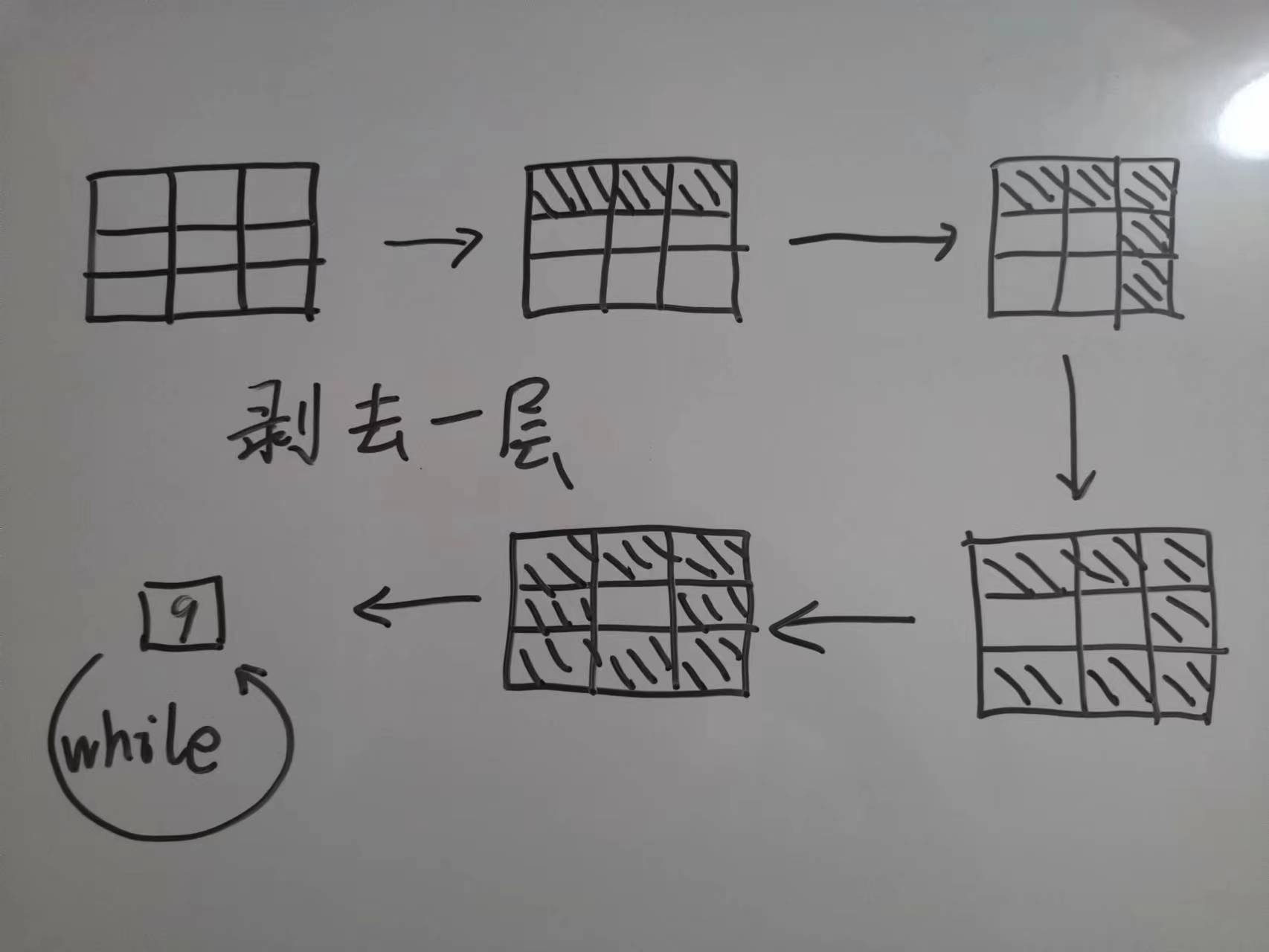
while 循环一次后,top、bottom、left、right 都更新到了 9 的位置,把 9 再当成一层,继续填充。