343. 整数拆分
假设正整数 i 可以拆分成 j 和 i - j,那么乘积可以是 j (i - j),但是 i - j 可能还能继续拆,那么乘积可以是 j (i - j 的拆分后的乘积最大值)。因此可以使用动态规划来解决这个重叠的子问题,定义 dp[i] 为将 i 拆分后得到的乘积最大值。对于 0 和 1 是无法拆分的,因此初始化为 0。dp 的循环就可以从 2 开始。拆分的 j 的范围是 1 ~ i - 1。内层循环就是在尝试拆 1 ~ i - 1 中的每个数,然后记录最大的值做 dp[i]。
有人可能会问为什么只考虑 i - j 可以拆,j 能不能拆呢?j 是可以拆的,只不过按我们的遍历顺序已经包含了拆分 j 的情况,因为 j 是从 1 开始遍历的,从前往后一点一点构建 dp 数组的。
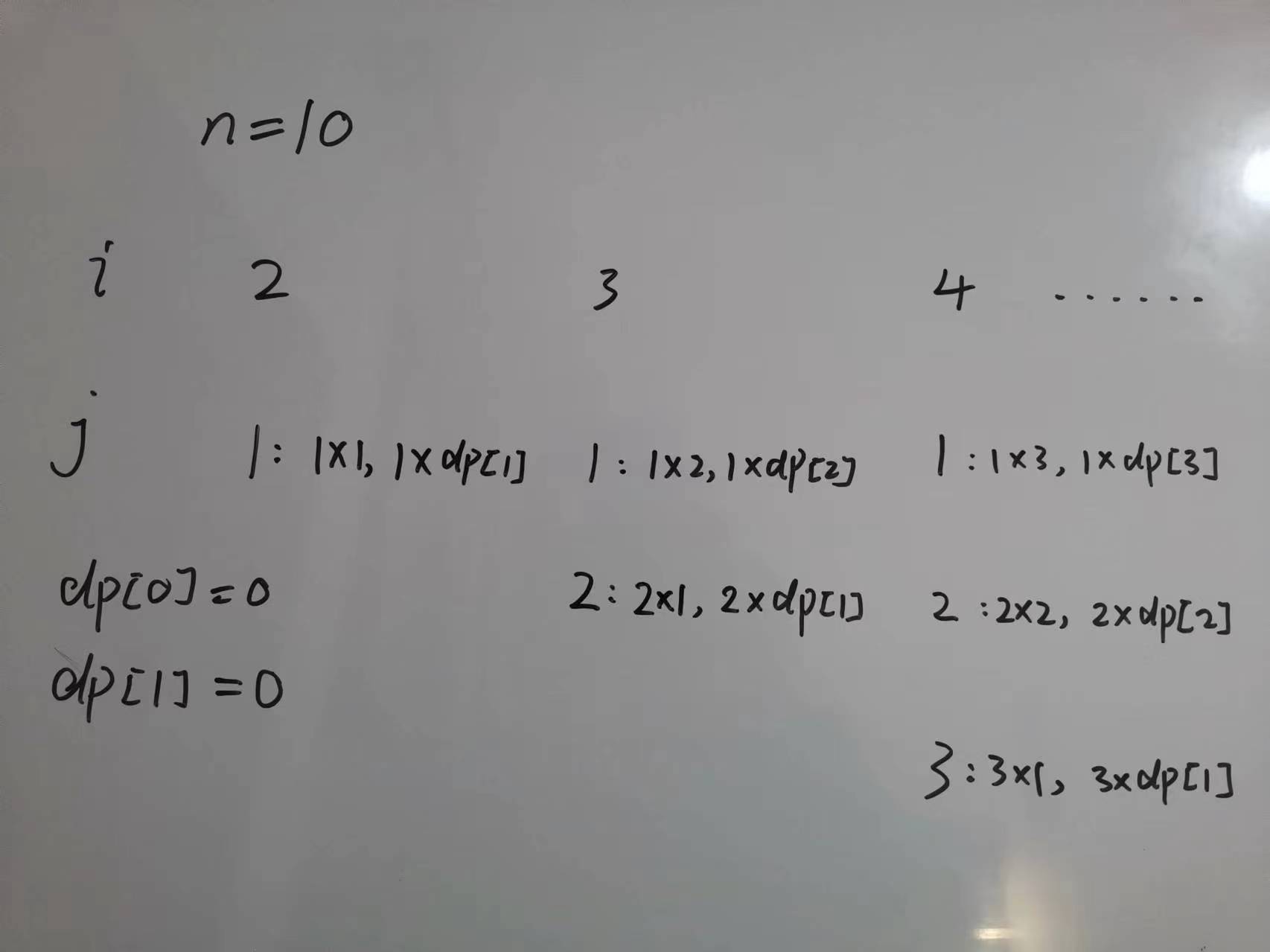
class Solution {
public int integerBreak(int n) {
int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 0;
for (int i = 2; i < dp.length; i++) {
int currMax = 0;
for (int j = 1; j <= i - 1; j++) {
currMax = Math.max(currMax, Math.max(j * (i - j), j * dp[i - j]));
}
dp[i] = currMax;
}
return dp[n];
}
}96. 不同的二叉搜索树
尝试用 1 ~ n 作为根节点构建二叉搜索树,看有几种情况,那么对于 n 位数来说,解法为各位数为根节点构成的二叉搜索树情况之和。如 n 为 3 时,总共的解法有 5 种,分别是以 1 为根节点的 2 种,2 为根节点的 1 种,3 为根节点的 2 种。
现在定义 dp[i],表示由 i 个节点组成(节点值从 1 到 i)且互不相同的二叉搜索树有 dp[i] 种。
因为是二叉搜索树,所以可以抽象出一模型来得出递推公式。假设以 j 为根节点,那么其左子树有 j - 1 个节点,右子树有 n - j 个节点。因此以 j 为根节点的二叉搜索树有 dp[j - 1] * dp[n - j] 种情况。
大家还要注意一个问题,那就是能构成的二叉搜索树的数量只和节点的个数有关,比如 1、2、3 和 5、6、7 虽然是两组不同的值,但是他们能构成的二叉树的总类是一样的,形状上是一样的。
class Solution {
public int numTrees(int n) {
int[] dp = new int[n + 1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
// 内部循环用来做累加,即以 1 ~ i 为根节点的二叉树的总类和
for (int j = 1; j <= i; j++) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
}
}