代码随想录算法训练营第二十二天 | 二叉搜索树的最近公共祖先、二叉搜索树中的插入操作

235. 二叉搜索树的最近公共祖先

leetcode
文档题解
视频题解

二叉搜索树，知识点联想：中序遍历、有序性、双指针（prev、curr）、划分区间，部分遍历（折半查找，根据有序性找前进方向）。

本题就是根据二叉搜索树的有序特征，抛弃不满足条件的区间，进行折半查找。

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) return null;
        if (root == p) return p;
        if (root == q) return q;

        // root 在中间
        if (root.val > p.val && root.val < q.val || root.val > q.val && root.val < p.val) return root;
        // root 在左边
        if (root.val > p.val && root.val > q.val) {
            return lowestCommonAncestor(root.left, p, q);
        }
        // root 在右边
        if (root.val < p.val && root.val < q.val) {
            return lowestCommonAncestor(root.right, p, q);
        }

        return null;
    }
}
// 递归精简版
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        // 这个判断可以不写，首先是题目要求，p、q 一定在树中，所以 root 不可能为空
        // 其次是递归的过程中，访问 left，right 是因为对应的方向有 p、q，所以也不可能为空
        if (root == null) return null;

        if (root.val < p.val && root.val < q.val) {
            return lowestCommonAncestor(root.right, p, q);
        } else if (root.val > p.val && root.val > q.val) {
            return lowestCommonAncestor(root.left, p, q);
        } else {
            // root 在 p、q 之间，或者就是 p、q 时的情况
            return root;
        }
    }
}
// 迭代法
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        // 本质还是不断划分区间，持续深入
        // 这里可以不用 curr，直接用 root
        TreeNode curr = root;
        while (curr != null) {
            if (curr.val < p.val && curr.val < q.val) {
                curr = curr.right;
            } else if (curr.val > p.val && curr.val > q.val) {
                curr = curr.left;
            } else {
                return curr;
            }
        }
        return null;
    }
}

701. 二叉搜索树中的插入操作

leetcode
文档题解
视频题解

二叉搜索树的节点插入不是作为根节点，就是作为叶子节点，核心操作还是划区间，按一条线深入。

// 递归法
class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) {
            return new TreeNode(val);
        }

        if (root.val < val) {
            // 保持右子树的衔接
            root.right = insertIntoBST(root.right, val);
        } else {
            // 保持左子树的衔接
            root.left = insertIntoBST(root.left, val);
        }

        return root;
    }
}
// 迭代法
class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) {
            return new TreeNode(val);
        }

        // 这里要用 curr 去遍历，因为最终结果要返回二叉树的根，所以不能用 root 遍历
        TreeNode curr = root;

        while (true) {
            if (curr.val < val) {
                // 向右找
                if (curr.right == null) {
                    curr.right = new TreeNode(val);
                    break;
                } else {
                    curr = curr.right;
                }
            } else if (curr.val > val) {
                // 向左找
                if (curr.left == null) {
                    curr.left = new TreeNode(val);
                    break;
                } else {
                    curr = curr.left;
                }
            }
        }

        return root;
    }
}
// 迭代法 - 记录父节点
class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) return new TreeNode(val);

        // 记录父节点
        TreeNode parent = null;
        TreeNode curr = root;

        while (curr != null) {
            // 每次遍历更新父节点
            parent = curr;
            if (curr.val < val) {
                curr = curr.right;
            } else {
                curr = curr.left;
            }
        }

        // 挂载节点
        if (val < parent.val) {
            parent.left = new TreeNode(val);
        } else {
            parent.right = new TreeNode(val);
        }

        return root;
    }
}

450. 删除二叉搜索树中的节点

leetcode
文档题解
视频题解

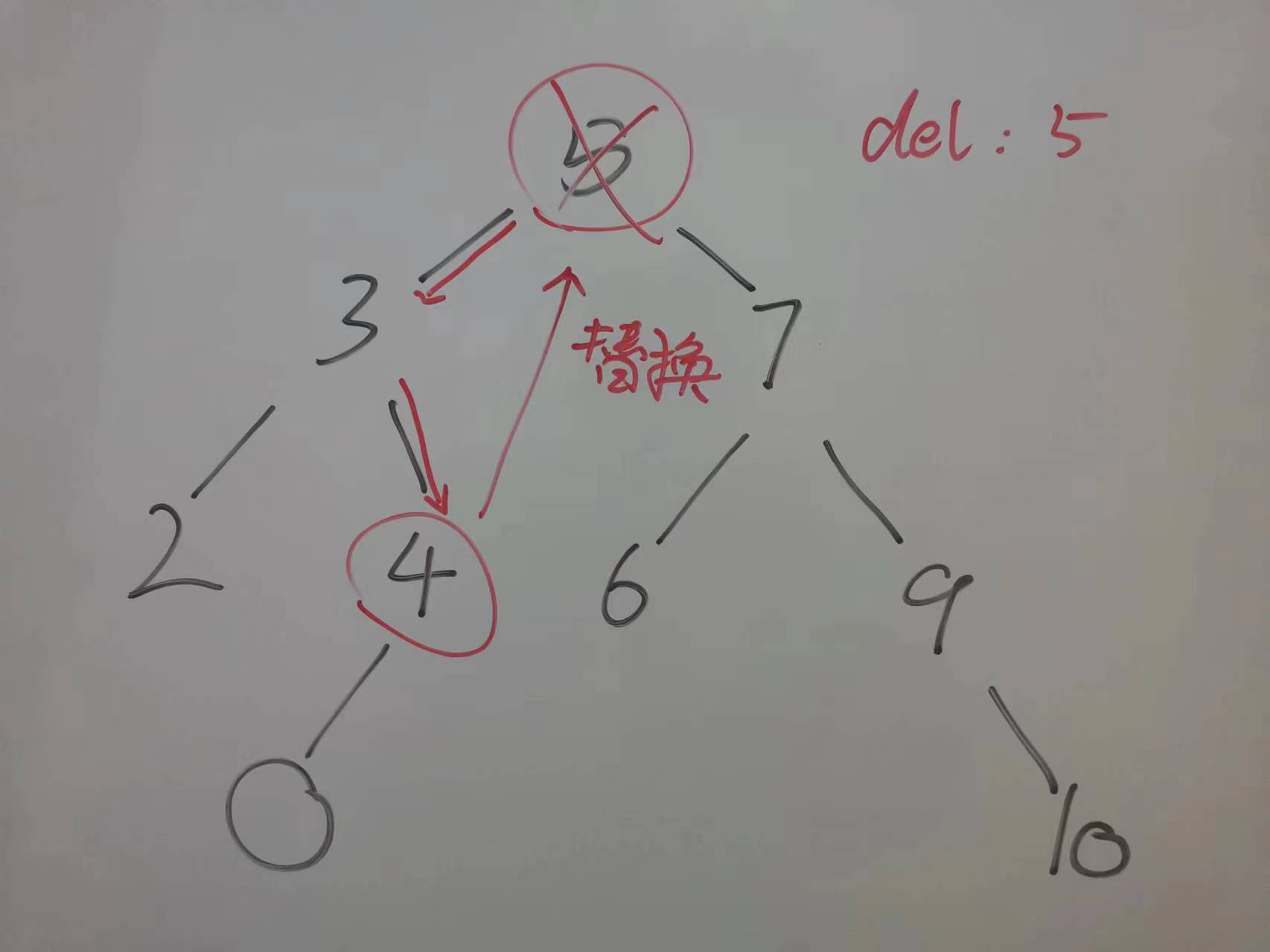
简单一句话，用待删除节点的左子树中最大的节点替换掉待删除的节点，或者用待删除节点的右子树中最小的节点替换掉待删除节点。

如图，删除 5，找到的左子树中最大的节点是 4，先递归删除 4，然后将 4 放到 5 的位置。

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) return null;

        if (key < root.val) {
            root.left = deleteNode(root.left, key);
        } else if (key > root.val) {
            root.right = deleteNode(root.right, key);
        } else {
            TreeNode leftMax = getMax(root.left);
            if (leftMax != null) {
                // 递归删除左子树中最大的节点
                root.left = deleteNode(root.left, leftMax.val);
                leftMax.left = root.left;
                leftMax.right = root.right;
                root = leftMax;
            } else {
                // 说明没有左子树，则直接使用右子树代替要删除的节点
                root = root.right;
            }
        }

        return root;
    }

    public TreeNode getMax(TreeNode root) {
        if (root == null) return null;

        while (root.right != null) {
            root = root.right;
        }

        return root;
    }
}

上面的思路和代码不够清晰，最好还是分情况考虑：

  1. 根节点为空，返回 null
  2. 待删除节点是叶子节点，返回 null
  3. 待删除节点的左子树为空，右子树不为空，返回右子树
  4. 待删除节点的右子树为空，左子树不为空，返回左子树
  5. 待删除节点的左右子树都不为空，则要找到左子树中最大的节点，将待删除节点的右子树接到最大值节点的右子树上，然后将新 root 指向老 root 的左子树，最后返回新 root
class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) return null;

        if (key < root.val) {
            root.left = deleteNode(root.left, key);
        } else if (key > root.val) {
            root.right = deleteNode(root.right, key);
        } else {
            // root 就是待删除的节点
            if (root.left == null) return root.right;
            if (root.right == null) return root.left;
            // 寻找左子树中的最大值
            TreeNode curr = root.left;
            while (curr.right != null) {
                curr = curr.right;
            }
            // 将待删除节点的右子树接到最大值节点的右子树上
            curr.right = root.right;
            // 新 root 就是老 root 的左子树
            root = root.left;
            // 返回新的 root
            return root;
        }

        return root;
    }
}

发表回复

您的邮箱地址不会被公开。 必填项已用 * 标注