104. 二叉树的最大深度

leetcode
文档题解
视频题解

二叉树节点的深度：该节点到树根的距离，从下到上。

二叉树节点的高度：该节点到叶子节点的最长距离，从上到下。

前序遍历可以求节点的深度，后序遍历可以求节点的高度。

二叉树的最大深度（高度）其实就是根节点的高度，因此可以使用后序遍历。

class Solution {public int maxDepth(TreeNode root) {if (root == null) return 0;

        int lh = maxDepth(root.left);
        int rh = maxDepth(root.right);

        // 以 root 为根的树的深度是左右子树中最大的深度 + 1
        return Integer.max(lh, rh) + 1;
    }
}

111. 二叉树的最小深度

leetcode
文档讲解
视频讲解

if (root == null) return 0;

        int ld = minDepth(root.left);
        int rd = minDepth(root.right);

        // 重点，二叉树的深度一定是要触及到叶子节点的
        // 如果只有右孩子，则最小深度要从右子树算起
        if (root.left == null && root.right != null) {return 1 + rd;}

        // 如果只有左孩子，则最小深度要从左子树算起
        if (root.right == null && root.left != null) {return 1 + ld;}

        return 1 + Integer.min(ld, rd);

222. 完全二叉树的节点个数

leetcode
文档题解
视频题解

遍历树，时间复杂度 O(n)。

// 后序遍历（递归）class Solution {public int countNodes(TreeNode root) {if (root == null) return 0;
        // 统计左右子树的节点数量，然后再加上根节点的数量
        int ls = countNodes(root.left);
        int rs = countNodes(root.right);
        return ls + rs + 1;
    }
}

// 层序遍历（迭代）class Solution {public int countNodes(TreeNode root) {if (root == null) return 0;
        int count = 0;
        Queue<TreeNode> q = new LinkedList<>();
        q.offer(root);
        while (!q.isEmpty()) {TreeNode node = q.poll();
            count++;
            if (node.left != null) {q.offer(node.left);
            }
            if (node.right != null) {q.offer(node.right);
            }
        }
        return count;
    }
}

题目强调了“完全二叉树”，可以使用以下解法。

完全二叉树的两种表现形式：满二叉树、普通完全二叉树（即最后一层没铺满）。

可以将完全二叉树看作是一些满二叉树 + 分支节点组成的，如下图：

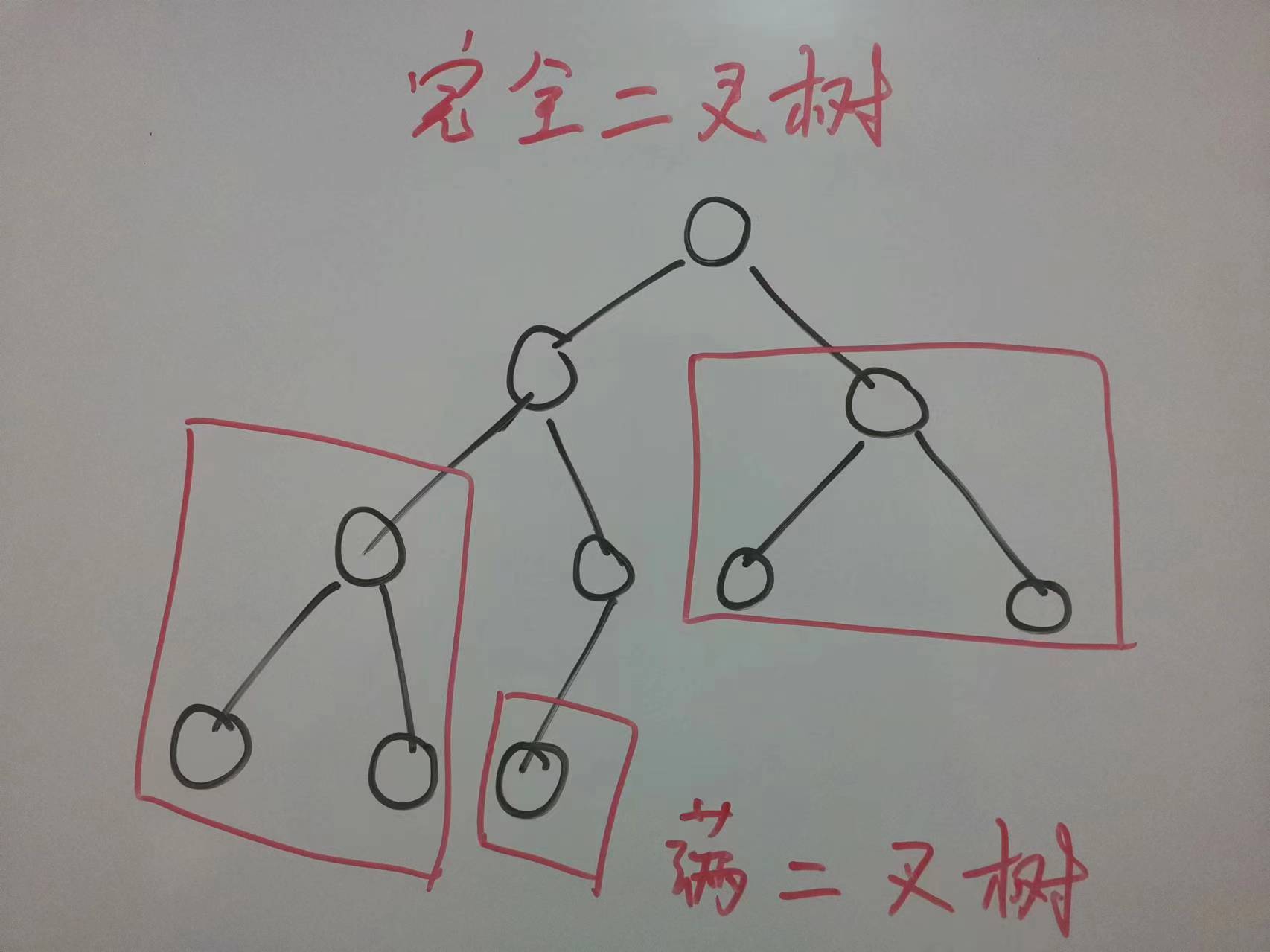
满二叉树的节点数量可以用公式计算：2 ^ 树的高度 - 1。

该题还是可以通过后序遍历的方式计算节点数量，只不过遇到满二叉树时可以通过公式提高计算速度。

if (root == null) return 0;

        TreeNode l = root.left;
        TreeNode r = root.right;
        int ls = 0;
        int rs = 0;

        while (l != null) {
            l = l.left;
            ls++;
        }

        while (r != null) {
            r = r.right;
            rs++;
        }

        // 判断是否为“满二叉树”// 使用公式计算满二叉树的节点数量
        if (ls == rs) {return (2 << ls) - 1;
        }

        return countNodes(root.left) + countNodes(root.right) + 1;