01 背包
给定一些物品,每个物品都有自己的重量和价值,再给定一个指定容量的背包,问如何在不超过容量限制的情况下使得背包中的价值最大。注意:每个物品只有一个,要么选,要么不选,因此是 01 背包。
我们先不考虑为什么这个问题可以使用动态规划(?)
按照动态规划的一般求解步骤:
- 先将问题拆分,将原问题抽象为当前阶段和前一阶段。
原问题是在 m 个物品中做选择,使容量为 n 的背包价值最大。那么子问题就是在 i 个物品中做选择,使容量为 j 的背包价值最大。可以这么拆分么,不太确定,那就先按下不表,以划分阶段的方式看看有没有什么苗头。
当前阶段是在前 i 个物品中做选择,前一个阶段就是在前 i - 1 个物品中做选择,那么每个阶段的答案就是选择的最大价值。当前阶段和前一个阶段的差别就是当前阶段引入了新的物品 i, 那么当前阶段要做哪种决策呢?
决策一,不选,那么当前阶段的答案就是上一个阶段的答案,即当前阶段我可以选第 i 个物品,但是我没选,那么这时最大价值就是上一个阶段的最大价值。有同学可能会说,不对呀,如果还有空间,选择了物品 i 价值一定会更大,为什么不选呢?同学们要注意,我们说的阶段是在 0 ~ i 个物品中做选择,而不是已经选择了 i 个物品。引入第 i 个物品,也就是说第 i 个物品可供选择,可能会影响上一个阶段的最大价值。比如上一个阶段的最大价值是 10,新引入的物品价值是 100,那么当前阶段的最大价值就一定是 110 么?未必,可能是 110,也可能是 100,还有可能是 10。如果剩余容量还能放下新物品,那么就加进来,答案是 110;如果背包剩余容量不够,但是总容量够,那么可以抛弃之前选择的,只选新物品,答案是 100;如果新物品的重量比背包容量还大,那么铁定是放不下了,所以答案还是上一个阶段的答案,即 10。由此,我们可以看出容量也会影响每一个阶段的答案。
决策二,选,那么最大价值就是当前物品的价值和...和什么?和剩余容量所能承载的最大价值!等等,这就是最大价值了么?经过决策一的分析,我们知道在当前容量的限制下,选择新物品获取的价值不一定比不选获取的价值大,因此要取二者中的较大值。
经过上面的分析,我们知道要选择的物品和容量限制都会影响各个阶段的解。因此我们确定,子问题就是 在 i 个物品中做选择,使容量为 j 的背包价值最大。
- 状态定义,即子问题的解
因此可以定义二维 dp 数组,dp[i][j] 表示 在 i 个物品中做选择,装满容量为 j 的背包时得到的最大价值。
- 状态转移
即当前阶段,在选择新物品得到的最大价值和不选新物品得到的最大价值中挑较大的哪个。状态转义方程如下:
// dp[i - 1][j] 是不选择物品 i,在 j 容量限制下,上一阶段的最大价值
// dp[i - 1][j - weights[i]] 是选择物品 i,但要知道在剩余容量 j - weights[i] 下,从剩余 i - 1 个物品中选择的最大价值
dp[i][j] = Math.max(dp[i - 1][j], values[i] + dp[i - 1][j - weights[i]]);- 初始化状态,方便直接调用状态转移方程,避免不必要的判断
根据状态转移方程可知当前状态只和前一个状态有关,在二维数组上看就是左上方部分,因此我们要初始化这里,不然还得加数组越界的处理。首先我们要考虑背包容量为 0 的情况,不然在 dp[i - 1][j - weights[i]] 时就得加额外的判断,因此初始化 dp 数组时多加一列。其次要初始化 dp 数组的第一行,不然在 dp[i - 1][xxx] 时就得加额外判断,第一行只能选择第一个物品,所以也好初始化,能放下就放,不放的话最大价值就是 0。
- 开始实现!
import java.util.Scanner;
class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// 物品数量
int m = sc.nextInt();
// 背包容量
int n = sc.nextInt();
// 物品重量
int[] weights = new int[m];
// 物品价值
int[] values = new int[m];
// 初始化物品重量
for (int i = 0; i < m; i++) {
weights[i] = sc.nextInt();
}
// 初始化物品价值
for (int i = 0; i < m; i++) {
values[i] = sc.nextInt();
}
int maxValue = dpSolution(weights, values, m, n);
System.out.println(maxValue);
sc.close();
}
public static int dpSolution(int[] weights, int[] values, int m, int n) {
// dp[i][j] 表示从 0 ~ i 个物品中选择,在容量限制为 j 的情况下能装取的最大收益
int[][] dp = new int[m][n + 1];
// 初始化 dp
// 容量为 0,价值为 0(第一列)
for (int i = 0; i < m; i++) {
dp[i][0] = 0;
}
// 只能选第一件物品时最大价值取决于第一件物品的重量
for (int j = 1; j <= n; j++) {
dp[0][j] = weights[0] <= j ? values[0] : 0;
}
// 开始递推
for (int i = 1; i < m; i++) {
for (int j = 1; j <= n; j++) {
if (weights[i] <= j) {
// 容量可以,那就选
dp[i][j] = Math.max(dp[i - 1][j], values[i] + dp[i - 1][j - weights[i]]);
} else {
// 容量不够,不能选
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[m - 1][n];
}
}01 背包滚动数组
滚动数组是动态规划中常见的一种状态压缩的方式。根据上面的状态转移方程可以看出当前阶段只与上一阶段有关,从二维数组中看就是第 i 层只关心第 i - 1 层的数据,前面几层的数据都不再使用了,而且 [i, j] 也不会在意 [i, j - 1] 的数据,所以一层处理完后完全可以将这一层的数据复制到下一层,即直接使用一维数组,在当前层上直接计算,下面请看图:

public static int dpSolution(int[] weights, int[] values, int m, int n) {
// dp[j] 表示容量为 j 的背包,能获得的最大价值
int[] dp = new int[n + 1];
// 初始化
// 容量为 0 时当然初始化为 0
dp[0] = 0;
// 容量不为 0 时,看递推公式,dp[j] 要和其他值做比较取最大
// 所以也初始化为 0,免得初始值大了,会覆盖本要求得的值
// 遍历
for (int i = 0; i < m; i++) {
// 背包要倒序遍历,正序遍历会出现物品被多次选择的情况
for (int j = n; j > 0; j--) {
// 有空间再放
if (weights[i] <= j) {
dp[j] = Math.max(dp[j], dp[j - weights[i]] + values[i]);
}
// 没空间 dp[j] 还是原来的 dp[j],不用设置
}
}
return dp[n];
}为什么遍历背包的时候要倒序?根据状态转移方程,dp[j] 的结果可能要取 dp[j - weights[i]],取前面已经计算过的结果本身没什么问题。正序遍历的话,物品在前面被选择了,但是因为 dp 数组是经过压缩的,如果在后面的遍历中再取 dp[j - weights[i]] 就说明又取了一次物品,这是不被允许的,参见上图中的 [0, 15, 30...],30 的出现就表明物品被选择两次了。
为什么二维数组的时候可以正序呢?因为二维数组没有压缩状态,取的状态都是上一层的,没有取本层的状态,如果取本层的状态也可能会发生重复。当前层即纳入了新物品,当前层的每个值在计算的时候都会考虑是否选择新物品,如果当前层后面的值计算的时候还要去取当前层前面的值,那就有可能会重复。
所以,背包的遍历要倒序!倒序的时候,前面的背包都还没选新物品,所以不怕重复。
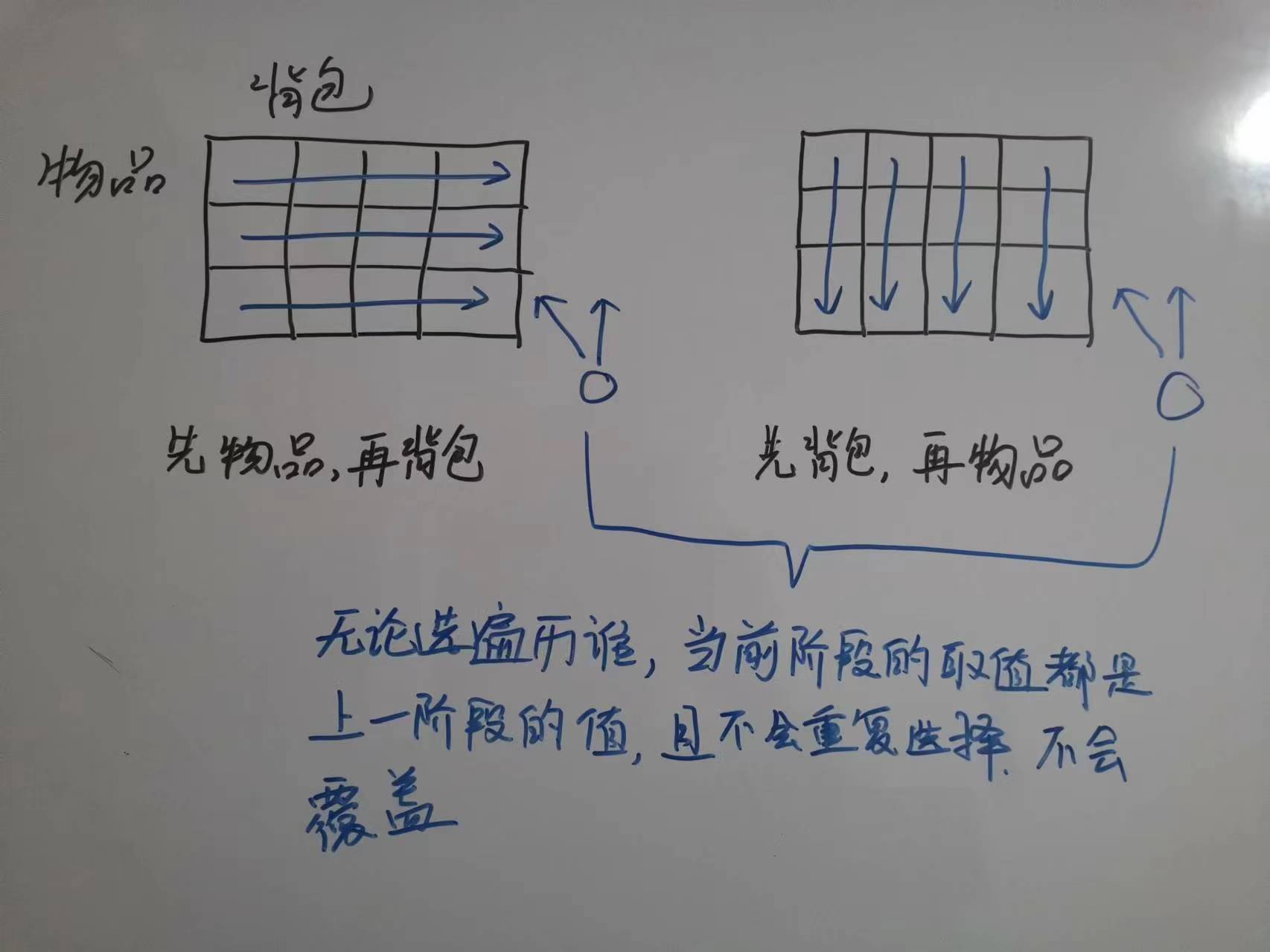
那么能不能先倒序遍历背包,再正序遍历物品呢?我们看下图:

可以看到交换顺序后,每个背包都只能选择一件物品了,因为遍历物品时都在修改同一个 dp[j],这也导致 dp[j - weights[i]] 失去了意义,因为当前层不会从上一层受益,这里的层表示背包,毕竟容量为 3 的背包怎么会从容量为 4 的背包中得到答案呢,这是倒序遍历背包导致的。既然背包和物品都交换顺序了,那能不能正序遍历背包呢?不能,还是会有重复选择:

那为什么二维数组的遍历顺序可以交换呢?看图: