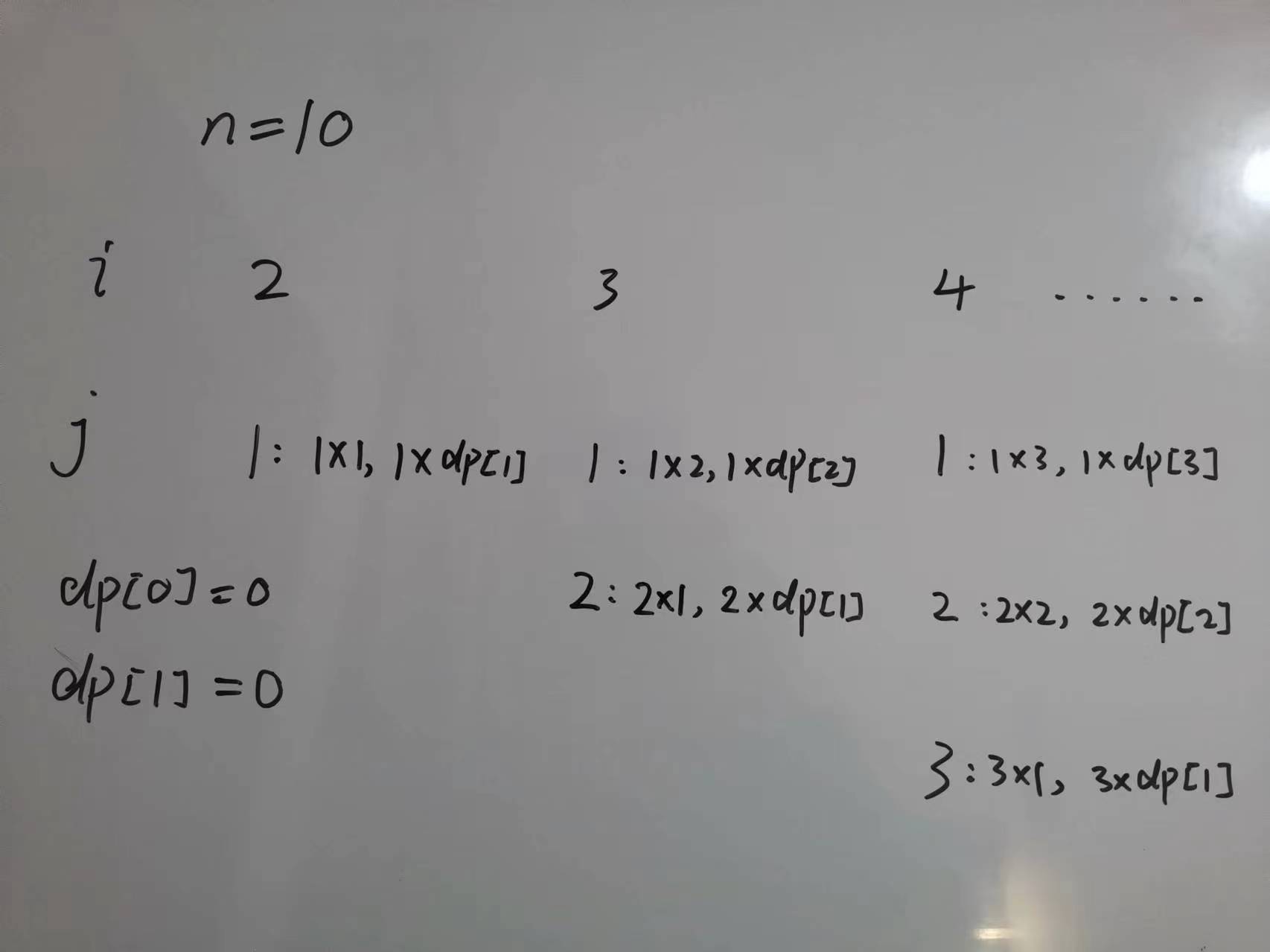代码随想录算法训练营第三十二天 | 买卖股票的最佳时机 II、跳跃游戏 I、II

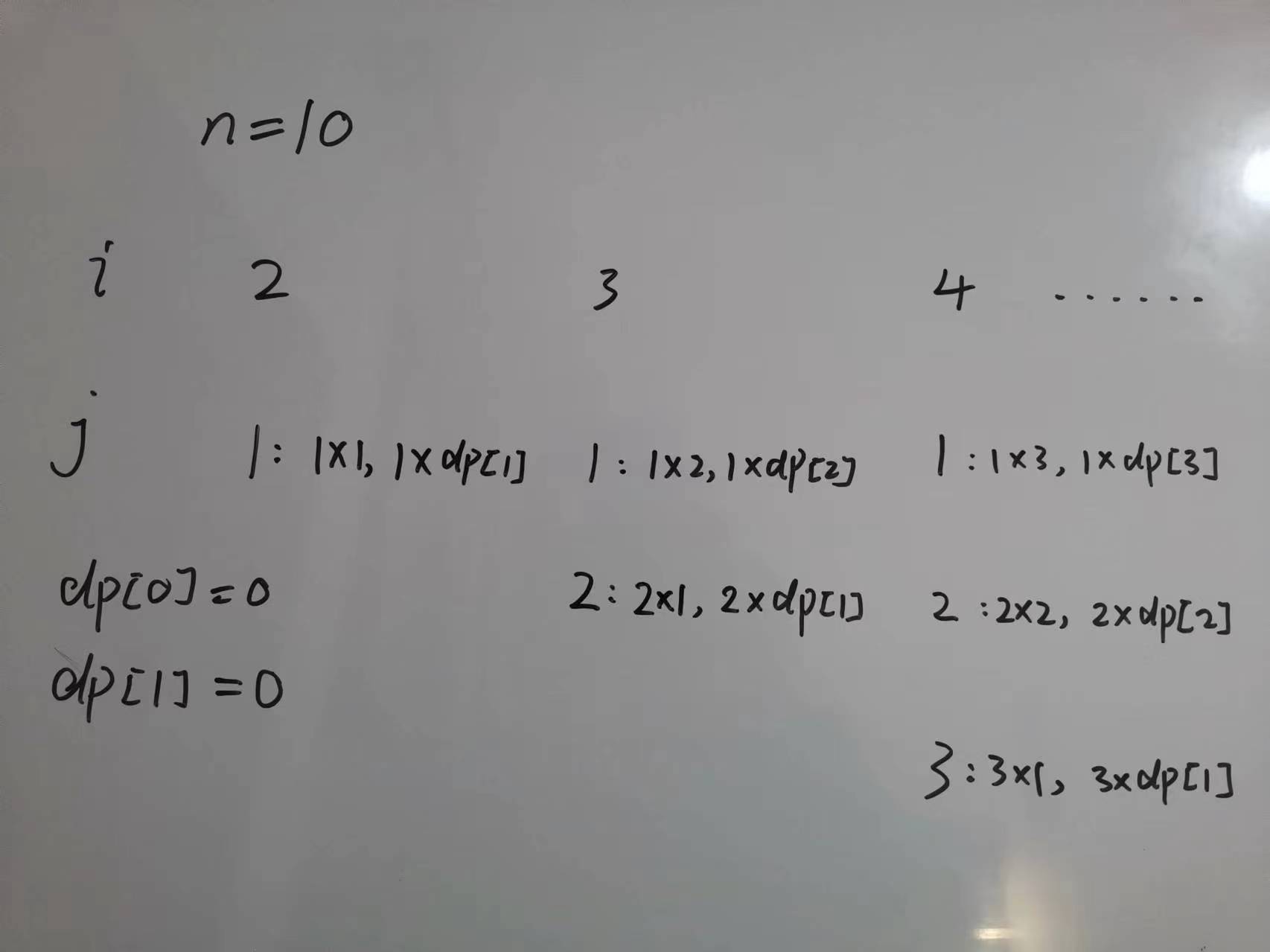
122. 买卖股票的最佳时机 II

leetcode
文档题解
视频题解

问题本质是在做决策，所以可以使用回溯算法来暴力搜索，问题就是会超时。

// 回溯算法
class Solution {
    int max = 0;
    public int maxProfit(int[] prices) {
        backtrace(prices, 0, 0, 0);
        return max;
    }

    /**
     *
     * @param prices 股价表
     * @param status 持有状态，0 未持有，1 持有
     * @param currProfit 当前利润
     * @param day 天数
     */
    public void backtrace(int[] prices, int status, int currProfit, int day) {
        if (day == prices.length) {
            // 决策树到头了，开始统计结果
            if (currProfit > max) {
                max = currProfit;
            }
            return;
        }

        // 不操作
        backtrace(prices, status, currProfit, day + 1);
        // 操作
        if (status == 0) {
            // 买入
            backtrace(prices, 1, currProfit - prices[day], day + 1);
        } else {
            // 卖出
            backtrace(prices, 0, currProfit + prices[day], day + 1);
        }
    }
}

贪心算法的思想就是选取当下的最优解，并期望得到全局的最优解。在这里就是第一天买，第二天买，如果是正收益的话。

// 贪心算法
class Solution {
    public int maxProfit(int[] prices) {
        int profit = 0;
        for (int i = 1; i < prices.length; i++) {
            if (prices[i] - prices[i - 1] > 0) {
                profit += prices[i] - prices[i - 1];
            }
        }
        return profit;
    }
}

55. 跳跃游戏

leetcode
文档题解
视频题解

也是一个决策问题，可以考虑回溯，不出意外的话又是超时。

class Solution {
    // 暴力回溯
    boolean ok = false;
    public boolean canJump(int[] nums) {
        backtrace(nums, 0);
        return ok;
    }

    /**
     * @param nums 数组
     * @param index 到达的位置
     */
    public void backtrace(int[] nums, int index) {
        if (index >= nums.length) return;
        if (index == nums.length - 1) {
            // 能访问到最后一个元素
            ok = true;
            return;
        }

        for (int i = 1; i <= nums[index]; i++) {
            // 剪枝
            if (ok) return;
            backtrace(nums, index + i);
        }
    }
}

先考虑一下，位置 x 如何才能到达位置 y？有两个条件，一是 x 是可到达的，二是 x 最远能到达的位置覆盖了 y。因此可以遍历数组，并维护一个当前能够到达的最远位置，如果当前遍历的元素超过了这个位置，说明是不可到达的，否则更新这个最远位置，并判断是否覆盖了最后一个元素，如果覆盖了，则说明能到达。

class Solution {
    public boolean canJump2(int[] nums) {
        // 当前最远到达的位置
        int maxIndex = 0;
        for (int i = 0; i < nums.length; i++) {
            // i 超出了最远到达的位置，说明 i 不可达
            if (i > maxIndex) return false;
            // 更新最远可以到达的下标
            maxIndex = Math.max(maxIndex, i + nums[i]);
            // 如果覆盖了最后的元素，说明可达
            if (maxIndex >= nums.length - 1) return true;
        }
        return false;
    }
}

45. 跳跃游戏 II

leetcode
文档题解
视频题解

决策问题，可以使用回溯暴力搜索，然后等着超时。

class Solution {
    int minCount;
    public int jump(int[] nums) {
        minCount = nums.length - 1;
        backtrace(nums, 0, 0);
        return minCount;
    }
    public void backtrace(int[] nums, int index, int currCount) {
        if (index >= nums.length) return;
        if (index == nums.length - 1) {
            minCount = Math.min(minCount, currCount);
            return;
        }

        for (int i = 1; i <= nums[index]; i++) {
            backtrace(nums, index + i, currCount + 1);
        }
    }
}

贪心，这个贪心策略是选择当前可跳跃范围内中能跳的更远的位置。

class Solution {
    public int jump(int[] nums) {
        // 上一步可以到达的最远位置
        int end = 0;
        // 下一步可以到达的最远位置
        int maxIndex = 0;
        int step = 0;

        for (int i = 0; i < nums.length - 1; i++) {
            // 维护下一步可以到达的最远位置
            maxIndex = Math.max(maxIndex, i + nums[i]);
            // 上一步最远就到 end 了，遍历到 end 说明这个范围内的下一次能到达的最远位置已经确定了，更新 end，并步数 +1
            if (i == end) {
                end = maxIndex;
                step++;
            }
        }

        return step;
    }
}

参考资料