代码随想录算法训练营第二十九天 | 非递减子序列、全排列 I II
491. 非递减子序列
重点:非递减、不重复、数组无序。
拿到本题时我上来就按照给定数组有序的思路去做了,因为给的第一个例子是个有序的数组(第二个根本没看),结果就错了。这才回想过来我连 “非递减” 都没做处理,太马虎了。

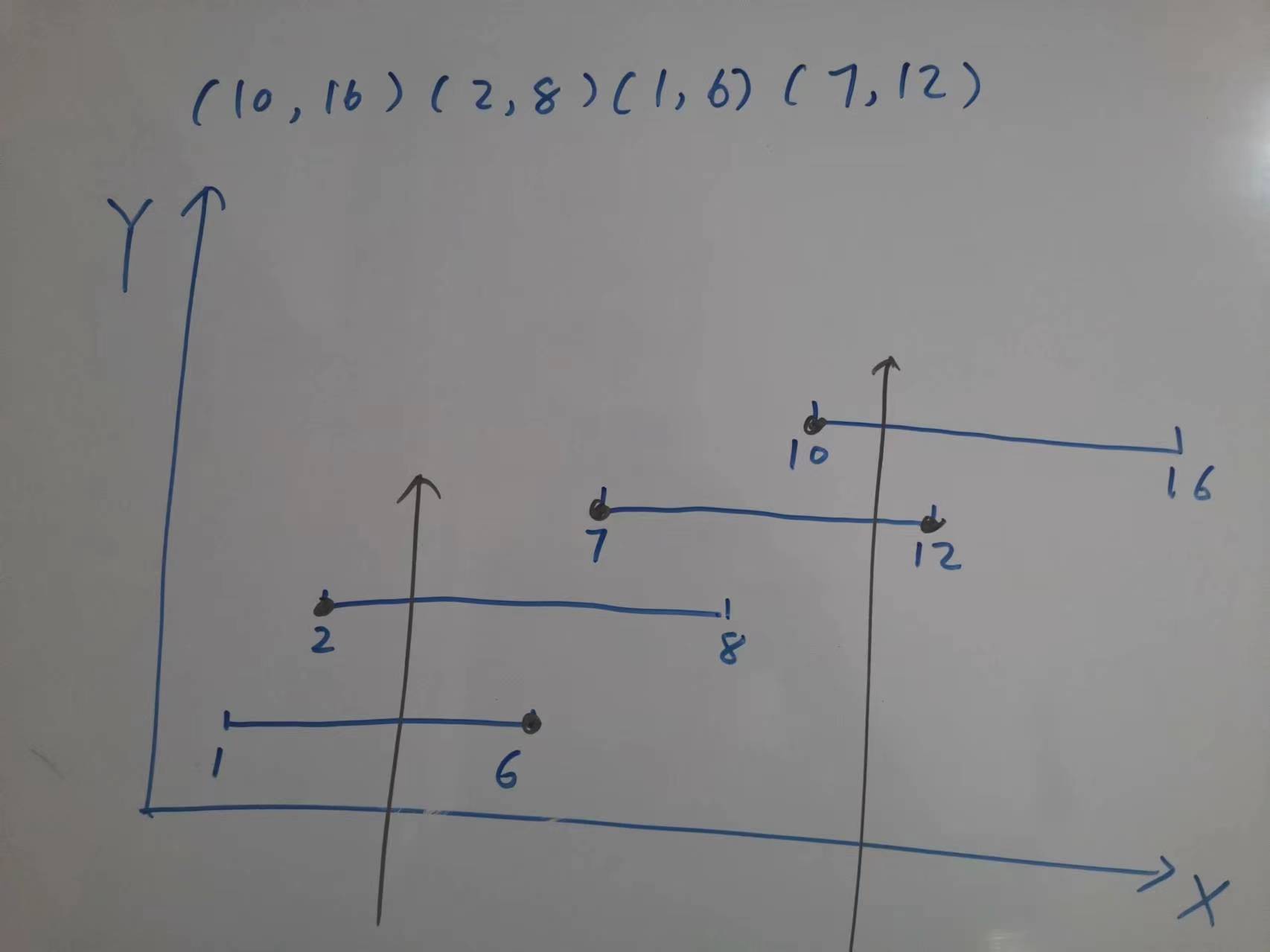
有序数组

无序数组
挨个思考技术点:
- 组合问题,需要使用 startIndex
- 单个结果中值不能重复,需要深入时要 i + 1
- 不能有相同的结果,需要去重,有序数组可以使用
if (i > startIndex && nums[i] == nums[i - 1]) continue;去重,但是本题不是有序数组,所以只能使用 used 数组或者 set - used 数组是处理当前层的,用于标记某个值在当前层是否被使用,其他层有各自的 used 数组,所以将当前层的 used 数组中的 nums[i] 标记为被使用即可,不需要回溯
按照这个思路写,就有答案了。
class Solution {
private List<List<Integer>> res;
private LinkedList<Integer> path;
public List<List<Integer>> findSubsequences(int[] nums) {
res = new LinkedList<>();
path = new LinkedList<>();
backtrace(nums, 0);
return res;
}
public void backtrace(int[] nums, int startIndex) {
if (path.size() >= 2) {
res.add(new LinkedList<>(path));
// 这里不能 return,还要继续向下找
}
// 题目给出了 nums 中数字的范围是 [-100, 100],所以声明一个 201 大小的数组
// 记录某个数字在本层是否使用过
boolean[] used = new boolean[201];
for (int i = startIndex; i < nums.length; i++) {
// 因为题目给的数组不是有序的,因此不能用此技巧
// 并且题目要求根据原数组的顺序获得非递减的序列,所以我们也不能排序
// if (i > startIndex && nums[i] == nums[i - 1]) continue;
// 如果 path 不为空,但是当前元素小于上一个元素,说明失序,就不能继续深入
// 或者当前元素在本层已经被使用过,那也不能继续了,因为要求结果不能重复
// nums[i] + 100 是因为数组没有负下标,所以往前移一下,
// 即 nums[i] == -100,在 used 中用 0 下标表示,nums[i] == 100,在 used 中用 100 下标表示
// 也算个技巧吧
if ((!path.isEmpty() && nums[i] < path.getLast()) || used[nums[i] + 100]) continue;
used[nums[i] + 100] = true;
path.add(nums[i]);
backtrace(nums, i + 1);
path.removeLast();
// 这里 used 不需要回溯,因为 used 只负责本层,下层有自己的 used
// 用过的元素设置为 true 就行,不用改回 false,否则就不起到去重的效果了
}
}
}时间复杂度:O(2^n),要求非递减的子序列,遍历所有子序列的时间复杂度是 O(2^n),每次 path 判空、获取最后元素、加入结果集的时间复杂度是 O(1),因此总的来说是 O(2^n)
空间复杂度:O(n),最坏情况是数组本来就是非递减的,因此 path 最长为 n,结果集最长为 2^n,但是结果集不被计算在空间复杂度内,因此是 O(n)
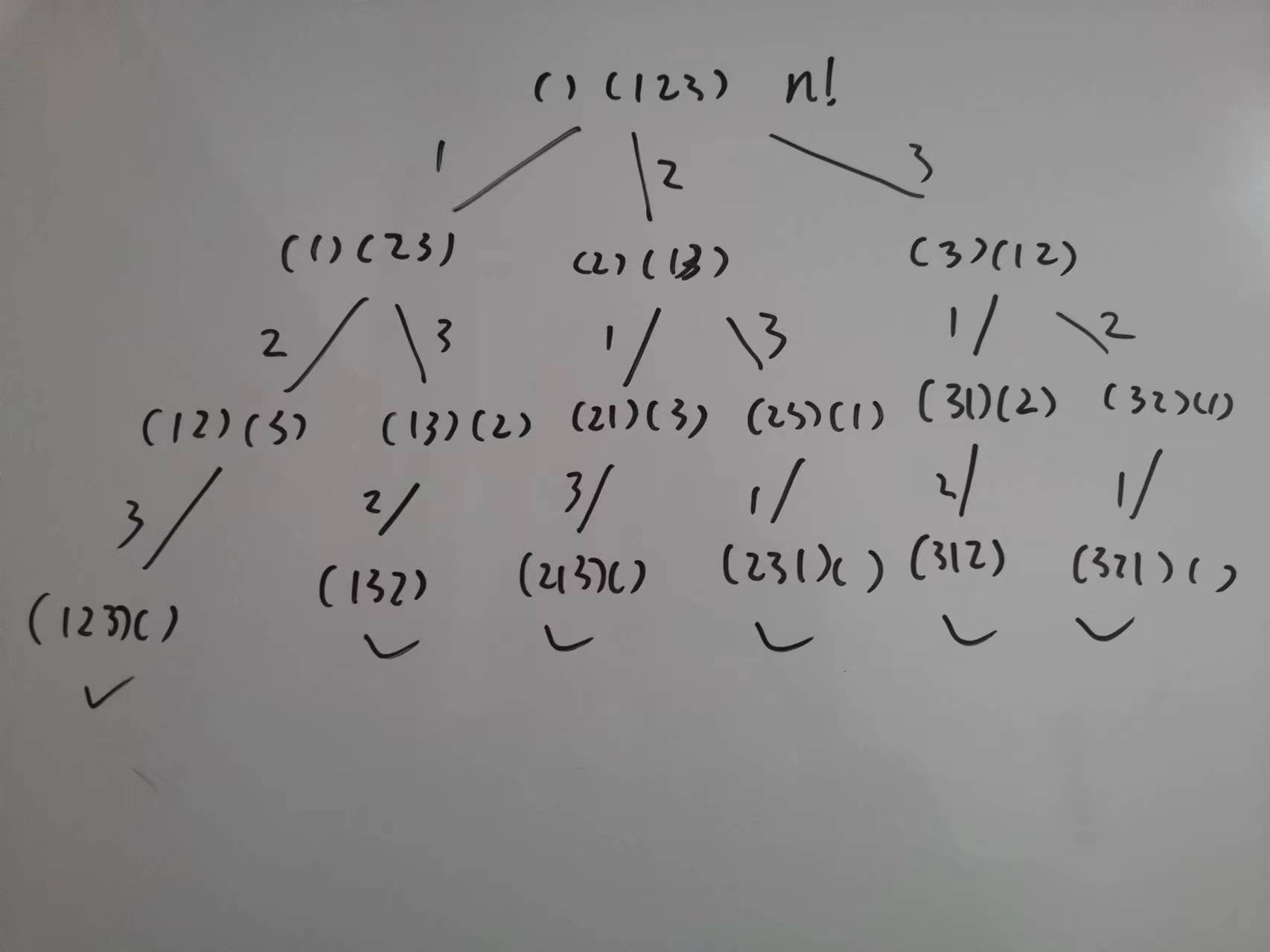
46. 全排列
全排列和组合的差距就在于全排列可以有重复的结果,不强调元素的顺序,如 [1, 2, 3] 和 [1, 3, 2] 都是结果。因此我们在 for 循环时不能像组合问题那样通过 startIndex 跳过前面所有的元素,而是让 i 每次都从 0 开始,已被 path 使用过的元素就跳过,没被使用过的继续参与排列,所以使用 used 数组,因为是看 path 是否使用过,所以这个 used 得是全局的。
used 记录此时 path 里都有哪些元素使用了,一个排列里一个元素只能使用一次。
class Solution {
List<List<Integer>> res;
LinkedList<Integer> path;
boolean[] used;
public List<List<Integer>> permute(int[] nums) {
res = new LinkedList<>();
path = new LinkedList<>();
used = new boolean[nums.length];
backtrace(nums);
return res;
}
public void backtrace(int[] nums) {
if (path.size() == nums.length) {
res.add(new LinkedList<>(path));
return;
}
// 因为是全排列,所以 i 要从头开始遍历,只是同一 path 中不能有重复的元素
for (int i = 0; i < nums.length; i++) {
// 通过全局 used 保证同一条 path 中没有重复的元素
if (used[i]) continue;
used[i] = true;
path.add(nums[i]);
backtrace(nums);
path.removeLast();
used[i] = false;
}
}
}时间复杂度:O(n!)
空间复杂度:O(n),path 和 used 的长度由 nums 的长度决定
47. 全排列 II
这次的数组中有重复的值,所以需要去重,横向的去重,即在 for 循环中,前面用过你这个元素了,这次不能再用。但是纵向是可以用的,因为这个元素有多个。那么如何确定当前元素是在横向中遍历还是在纵向中遍历呢,这里有个技巧,看 used 数组,如果 nums[i] == nums[i - 1] 且 used[i - 1] 为 true,说明 i 和 i - 1 在同一 path 上,也就是纵向,因此虽然是重复值,但是 i 是可以使用的;如果 used[i - 1] 为 false,说明前一个值已经回溯了,已经被使用过了,所以 i 是不可以被使用的,否则会有重复的答案。
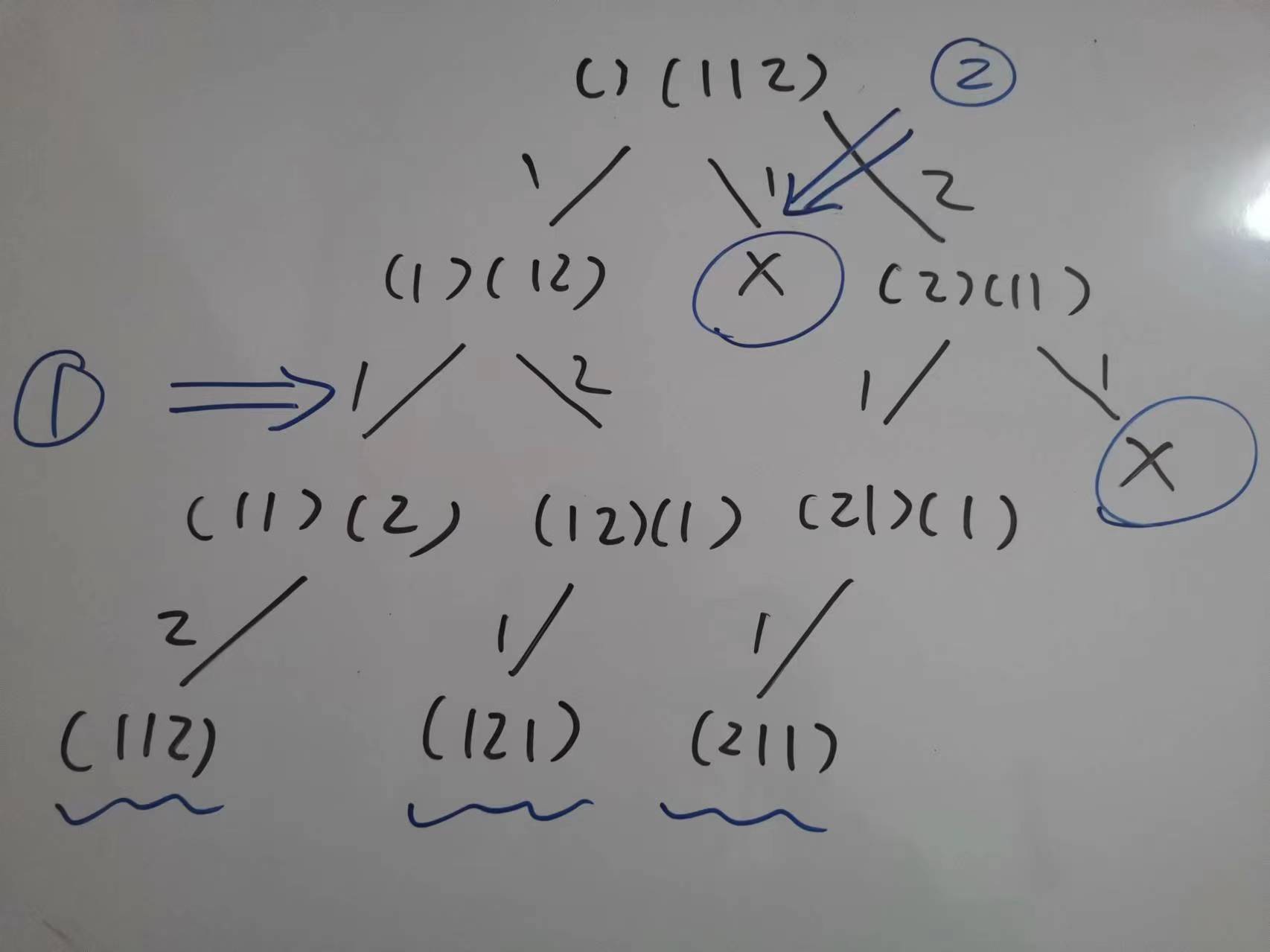
如上图中的序号 1,这个 1 可以使用是因为前一个 1 的 used 是 true,这两个 1 处于同一个 path。而序号 2 中,这个 1 不可以使用是因为前一个 1 的 used 是 false,前一个 1 已经被使用,used 回溯成了 false,因此这个 1 不能再次被使用了,从而实现了去重。
class Solution {
List<List<Integer>> res;
LinkedList<Integer> path;
boolean[] used;
public List<List<Integer>> permuteUnique(int[] nums) {
res = new LinkedList<>();
path = new LinkedList<>();
used = new boolean[nums.length];
// 去重一定要对元素进行排序,这样我们才方便通过相邻的节点来判断是否重复使用了
Arrays.sort(nums);
backtrace(nums);
return res;
}
public void backtrace(int[] nums) {
if (path.size() == nums.length) {
res.add(new LinkedList<>(path));
return;
}
for (int i = 0; i < nums.length; i++) {
// 重点
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) continue;
if (used[i]) continue;
used[i] = true;
path.add(nums[i]);
backtrace(nums);
used[i] = false;
path.removeLast();
}
}
}可以得出一个规律:对 树层 中前一位去重,就用 used[i - 1] == false,如果要对 树枝 前一位去重用 used[i - 1] == true。
您可能也喜欢

西什库天主堂闲游
2023年10月22日
代码随想录算法训练营第三十八天 | 斐波那契数、爬楼梯、使用最小花费爬楼梯
2024年3月17日