理论基础
先深入，再返回。
回溯是递归的副产品，只要有递归，就会有回溯。
回溯实际上是在做暴力穷举，算法效率并不高。
回溯法的本质是借用递归来解决 for 循环嵌套的问题，当某个问题需要多次嵌套 for 循环，且无法控制嵌套的深度时，就该考虑使用回溯算法了。
使用场景：
- 组合问题：n 个数中按照一定的规则，找到 k 个数的集合
- 排列问题：n 个数的全排列
- 切割问题：一个字符串按一定的规则，有几种切割方式（组合的一种）
- 子集问题：n 个数的集合中有多少符合条件的子集（组合的一种）
- 棋盘问题：n 皇后，数独等
解题模板
// 递归函数
void backtrace(选择列表，路径，结果集...) {
if (结束条件) {
将已做的选择添加进结果集
// 有时不需要，看情况
return;
}
// for 循环，回过头做新一轮决策，每一轮有好几层决策
for (遍历剩余的选择) {
执行选择操作
// 递归，做下一层的决策
backtrace(选择列表，路径，结果集...)
回退选择操作
}
}解题重点 - 画决策图
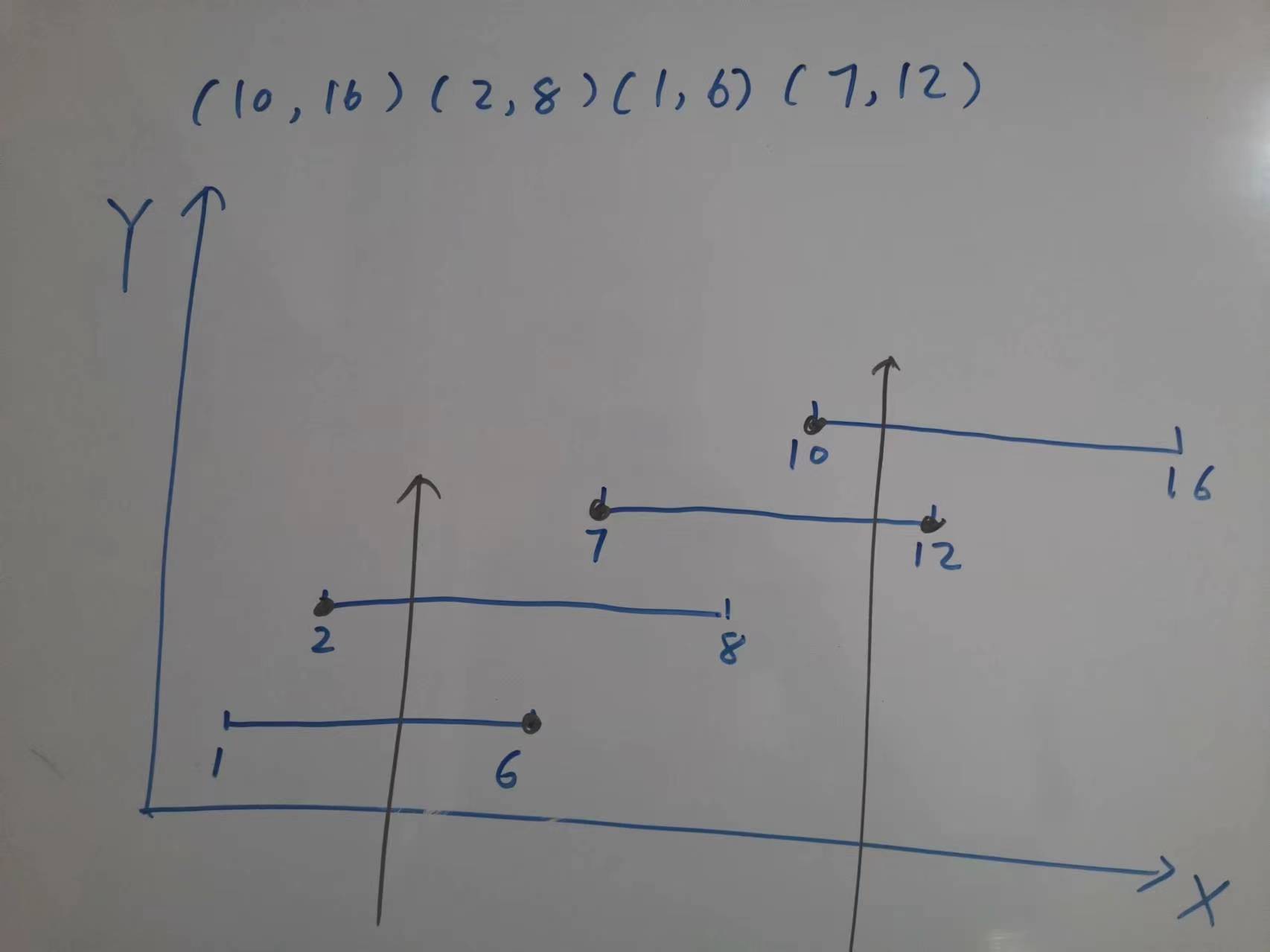
决策图是一个非常重要的工具，它展示了每一步做的决策，以及剩余的可选方案。如 77. 组合 的决策图：
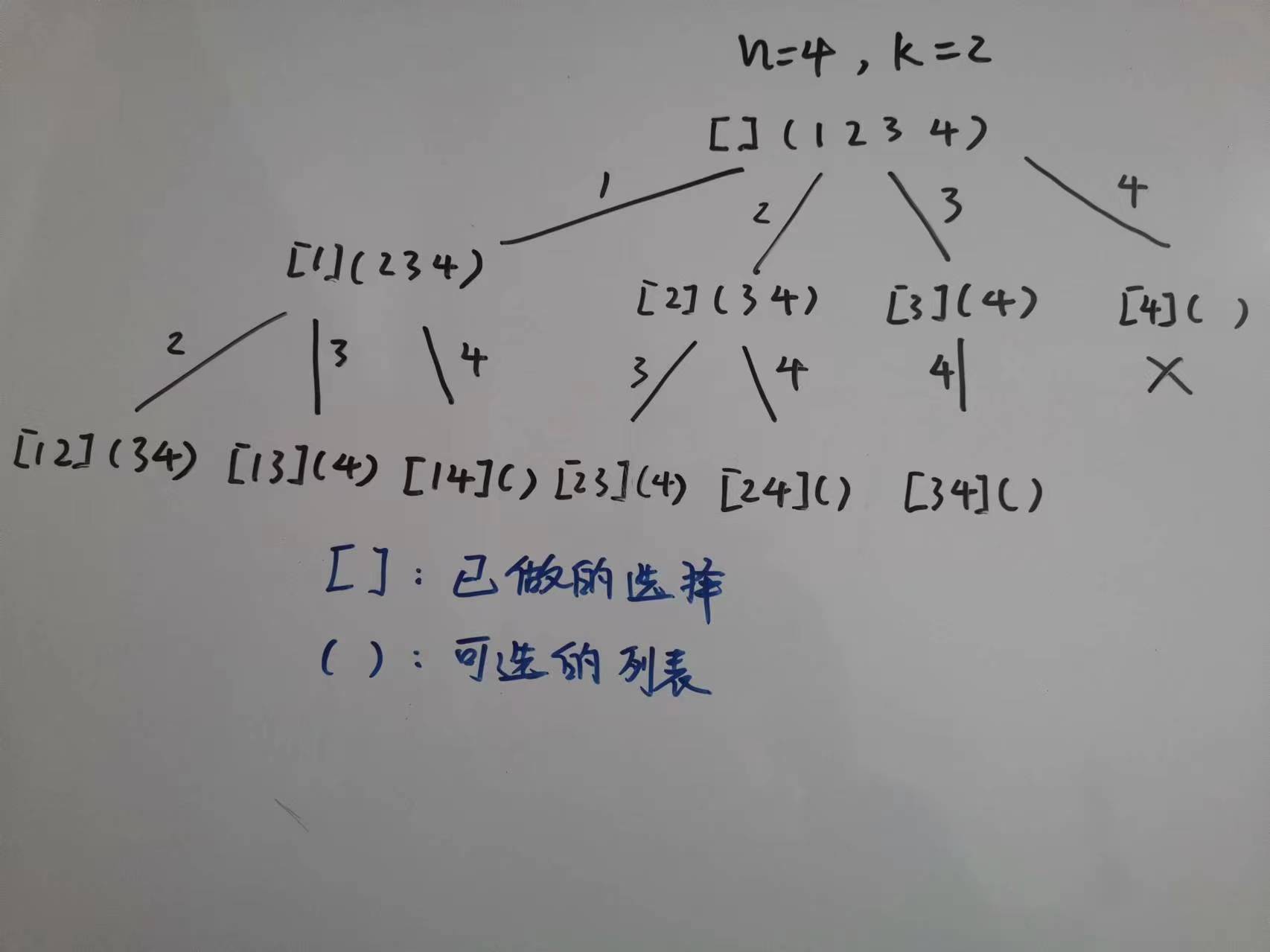
决策图的节点表示了某次决策的状态（已选择了哪些，还有哪些可选），边表示做的决策。
选择列表的长度决定了决策树（每个节点）的宽度，题目的限制条件决定了决策树的深度。
对应到模板中，横向的是 for 循环，表示树层上的选择，纵向的是递归，表示树枝上的选择。一般的剪枝操作就是在 for 循环上做手脚。
组合问题
组合问题要求结果不能重复，也就是说结果和元素的顺序无关，[1, 2, 3] 和 [3, 2, 1] 是同一个答案。
组合问题给出的选择列表（就是题目给的集合）可能有重复元素，也可能没有，有重复元素的话还要去重。
因为结果不能重复，因此组合问题的递归函数一般需要一个 startIndex 用来标志 for 循环的起点，即前面使用过的元素不应该再被使用，参考下面的代码：
void backtrace(int[] nums, int startIndex) {
if (结束条件) {
收集答案;
return;
}
// for 循环从 startIndex 开始遍历选择列表中的元素
// startIndex 前的都被使用过了
for (int i = startIndex; i < nums.length; i++) {
操作当前元素;
// 如果每一个答案中允许有重复的元素，如 [1, 1, 1] 是一个答案，则这么写 backtrace(nums, i)
// 如果不允许，那就 backtrace(nums, i + 1)，i + 1 表示从下一个元素开始
backtrace(nums, i + 1);
撤回对当前元素的操作;
}
}上面代码也是选择列表中没有重复元素的通用解法，如果选择列表中有重复的元素，那么还需要去重，去重的关键是先对选择列表进行 排序，让相同的元素聚集在一起，方便操作。代码如下：
// 定义全局 used，去重的重点
boolean[] used;
void backtrace(int[] nums, int startIndex) {
if (结束条件) {
收集答案;
return;
}
for (int i = startIndex; i < nums.length; i++) {
// 如果当前元素和前面的元素相同，且 used[前] 为 false，说明回溯过，即前面的元素被使用过
// 那么当前元素就不能再用了
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) continue;
used[i] = true;
path.add(nums[i]);
backtrace(nums, i + 1);
path.removeLast();
used[i] = false;
}
}其实完全可以不用 used，直接用 startIndex 就可以。
void backtrace(int[] nums, int startIndex) {
if (结束条件) {
收集答案;
return;
}
for (int i = startIndex; i < nums.length; i++) {
// 关键，如果当前元素和前一个元素相同，就不用处理当前元素了，因为上一个已经处理过了
// 注意：这里是 i > startIndex，而不是 i > 0，因为 i > startIndex 后才可以找前一个元素，
// i == startIndex 时，本层 for 循环才刚开始，还没有 “上一个” 元素。仅仅是 i > 0 的话，nums[i - 1] 可能是其他层的元素。
if (i > startIndex && nums[i] === nums[i - 1]) {
// 看情况，可以是 continue，也可以是 break
}
// ...
}
}这里再强调一下去重，有两个概念上的重复，一个是组合内，一个是组合之间。
组合内重复，也成为树枝重复，即 [1, 1, 2]，1 是可以重复的，在深层递归中是可以选择前面已经使用过的元素的。如果 nums[i] == nums[i - 1] && used[i - 1] == true，前一个相同的元素还在 path 中，说明是树枝重复。
组合之间重复，也称为树层重复，是指 [1, 2, 3] 和 [3, 2, 1] 是重复的，是同一个答案，在 for 循环中可以使用之前使用过的元素。如果 nums[i] == nums[i - 1] && used[i - 1] == false，即前一个相同的元素回溯了，已经从 path 中退出了，说明是树层重复。
这两种重复都可以在决策树上找到对应的表示，组合内重复表现在纵向上，组合间重复表现在横向上。
组合问题均不允许组合之间重复，否则就不叫组合问题了。所以我们讲的去重是指组合之间去重，即 树层之间去重。
前面我们说了 startIndex，但并不是所有的组合问题都要用 startIndex，一般这么考虑，如果题目要求从一个集合中选出所有满足条件的组合，那么就需要用 startIndex，如果是从多个集合中选择，就可以不使用，如 17. 电话号码的字母组合，这是个特殊的例子。
切割问题
本质上还是组合问题，使用 startIndex 当作切割线，取 [startIndex, i] 片段。
子集问题
子集问题本质还是组合问题，但是和组合问题不同的地方在于收集结果的时机。组合问题收集结果一般是在满足指定的条件后，而子集问题收集结果是在任意一个节点的时候，即每次 path 加入一个值，就将当前的 path 视作一个结果。
如果选择列表里面有重复的元素，那么去重的逻辑就是 i > startIndex && nums[i] == nums[i - 1]。
递增子序列
这个要单独拿出来，虽然也是子集问题，但是它的去重逻辑就不一样了。一般遇到去重的问题都需要对选择列表进行排序，但是本题是要求递增的子序列，不能排序，排序会打乱现有的顺序。那怎么做呢？实际上还是借助 used 数组，但是和之前的 used 数组不太一样，看下图：
我们看到方框中的 7 就是重复的元素，因为在这一层 7 已经被访问过了，所以不能再使用了，因此在每一层增加一个 used 数组，来记录本层元素的访问情况，因为只负责本层，所以也不需要参与回溯。
你可能会问，在本层设置 used 不能解决重复的问题吧，会不会出现这种情况，假设选择列表是 [1, 2, 1, 2]，前面已经访问过 [1, 2]，下次再访问 [2, 1]？
不会！
因为题目要求是有序的，所以递归时也是找那些能够满足顺序条件的元素进行递归，如上图 path 为 [4, 7] 时就不会再纳入 6。
不过上面提到的问题在一般的组合问题中确实会发生，但是本题特殊就特殊在有序上，所以可以采用当前层的 used 数组这种做法，纯属是巧了。下面举个一般的组合问题，不排序，只是用本层yi used 数组的情况：
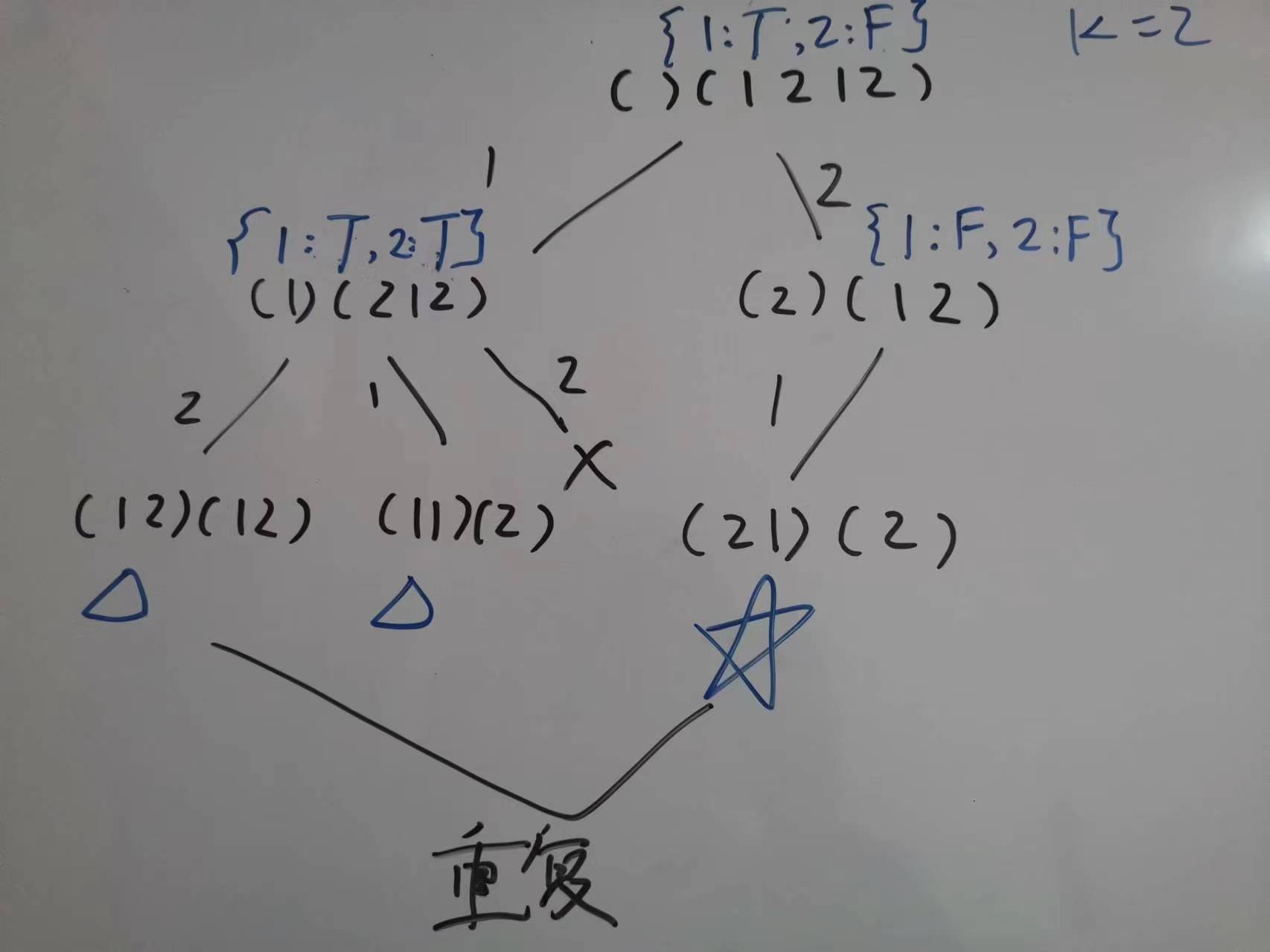
看到第二条第二层没，此时的 1 是 false，表示没被使用过，于是选了 1，得到了解 [2, 1]，和 [1, 2] 重复。
可能还会有人问，那如果也不排序，但是使用全局的 used 行不行？不行，请看 VCR：
这也对应了我们上面说的树枝重复和树层重复，这么做是会丢掉树枝重复的情况的。
因此，一般的组合问题的去重还是得先排序。然后 i > startIndex && nums[i] == nums[i - 1] && used[nums[i - 1]] == true 是树枝重复，i > startIndex && nums[i] == nums[i - 1] && used[nums[i - 1] == false] 是树层重复。
排列问题
排列问题关心顺序，即 [1, 2, 3] 和 [3, 2, 1] 是不同的答案，例如这层选了 3，下层仍需要选择 1，因此不需要 startIndex 控制 for 循环的起始条件，循环每次都从 0 开始，但是已选择过的元素（path 中的）不能再选了，所以需要全局 used 数组控制。
如果选择列表中有重复的元素，那么去重的方式和之前一样，树层去重。